题目内容
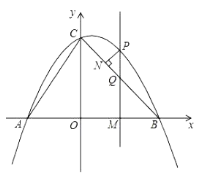
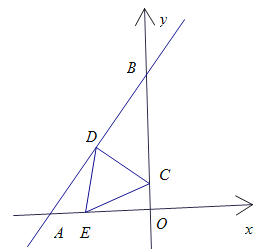
【题目】已知直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.点C在
轴相交于点B.点C在![]() 轴上运动,作CD⊥AB,垂足为D.点E为
轴上运动,作CD⊥AB,垂足为D.点E为![]() 轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
轴上一动点,点E关于CD中点的中心对称点为点F.设点C的坐标为(0,n).
(1)用n表示线段CD的长;
(2)当OC=1时,若点F落在直线y轴上,求此时点E的坐标;
(3)在点E的运动过程中,若存在唯一的位置,使得四边形CEDF为矩形,请直接写出点C的坐标
【答案】(1)![]() ;(2)
;(2)![]() ;(3)C的坐标为(0,0)或(0,
;(3)C的坐标为(0,0)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() )
)
【解析】
(1)先求出A,B坐标,然后表示出BC,OA,BA,再证明△BCD∽△BAO,得出![]() ,即可求出CD;
,即可求出CD;
(2)先求出CD的解析式,然后联立CD和AB的解析式得出D的坐标为,设CD的中点为G,得出G的坐标为(![]() ),然后根EF关于G对称,且F在y轴,可求出答案;
),然后根EF关于G对称,且F在y轴,可求出答案;
(3)根据题意得要想让四边形CEDF为矩形,则有C,E,D,F四点共圆,可推出四种情况①点C与点O重合;②点C在线段OB上;③点D与点A重合;④点C在y负半轴上,且以CD为直径的圆与x轴相切,分别讨论即可.
解:(1)由题意可求出直线![]() 与
与![]() 轴相交于点A的坐标为(-3,0),与
轴相交于点A的坐标为(-3,0),与![]() 轴相交于点B的坐标为(0,4),
轴相交于点B的坐标为(0,4),
∵点C的坐标为(0,n),
∴BC=4-n,OA=3,BA=5,
∵CD⊥AB,∠DBC=∠ABO,
∴△BCD∽△BAO,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵OC=1,
∴C(0,1),
∵CD⊥AB,
∴kCD·kAB=-1,
∵kAB=![]() ,
,
∴kCD=![]() ,
,
∴设CD的解析式为y=![]() x+b,
x+b,
将C代入得b=1,
∴CD的解析式为y=![]() x+1,
x+1,
联立CD和AB的解析式得: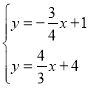 ,
,
解得: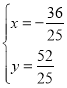 ,
,
∴D的坐标为(![]() ),
),
设CD的中点为G,
∴G的坐标为(![]() ),
),
∵EF关于G对称,且F在y轴,
∴xG-xE=0-xG,
xE=![]() ,
,
∴![]() ;
;
(3)要想让四边形CEDF为矩形,
根据矩形的性质可知这四点共圆,圆心为CD中点G,
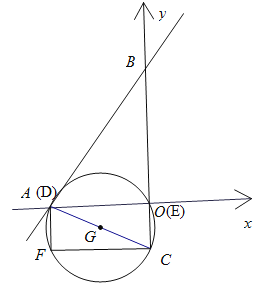
如图,可得出四种情况,
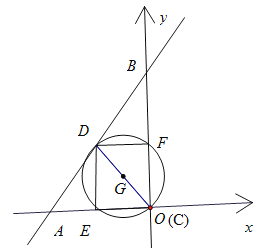
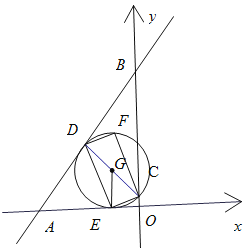
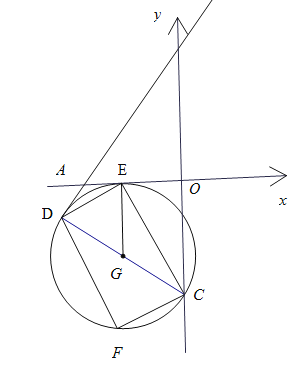
①点C与点O重合,此时C的坐标为(0,0);
②点C在线段OB上,此时以CD为直径的圆与x轴相切,
设CD的解析式为:y=![]() x+n,
x+n,
联立CD和AB的解析式可得D的坐标为(![]() ),
),
∴点G的坐标为(![]() ),
),
∵以CD为直径的圆与x轴相切,
∴GE⊥x轴,
∴点E的横坐标与点G相同,
∴E的坐标为(![]() ,0),
,0),
∵![]() CD=GE,
CD=GE,
∴可得![]() ×
×![]() =
=![]() ,
,
解得n=![]() ,
,
∴C的坐标为(0,![]() );
);
③点D与点A重合,
此时D的坐标为(-4,0),E的坐标为(0,0),
∵四边形
∴根据勾股定理可得![]() =
=![]() ,
,
解得n=![]()
∴C的坐标为:(0,![]() );
);
④点C在y负半轴上,且以CD为直径的圆与x轴相切,
由②可得此时![]() ×
×![]() =-
=-![]() ,
,
解得n=![]() ,
,
∴C的坐标为:(0,![]() );
);
综上,C的坐标为:(0,0)或(0,![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() ).
).

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】某大学生利用40天社会实践参与了某加盟店经营,他销售了一种成本为20元/件的商品,细心的他发现在第![]() 天销售的相关数据可近似地用如下表中的函数表示:
天销售的相关数据可近似地用如下表中的函数表示:
销售量 | 销售单价 | |
| 当 | 当 |
(1)求前20天第几天获得的利润最大?最大利润是多少?
(2)求后20天第几天获得的利润最大?最大利润是多少?
(3)在后20天中,他决定每销售一件商品给山区孩子捐款![]() 元(
元(![]() 且
且![]() 为整数),此时若还要求每一天的利润都不低于160元,求
为整数),此时若还要求每一天的利润都不低于160元,求![]() 的值.
的值.