Question

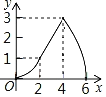
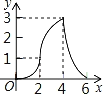
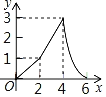
【题目】某大学生利用40天社会实践参与了某加盟店经营，他销售了一种成本为20元/件的商品，细心的他发现在第天销售的相关数据可近似地用如下表中的函数表示：

销售量	销售单价
	当时，单价为	当时，单价为40

（1）求前20天第几天获得的利润最大？最大利润是多少？

（2）求后20天第几天获得的利润最大？最大利润是多少？

（3）在后20天中，他决定每销售一件商品给山区孩子捐款元（且为整数），此时若还要求每一天的利润都不低于160元，求的值．

Answer 1

【答案】（1）前20天中，第15天获得利润最大，最大利润是元；（2）后20天中，第21天获得利润最大，最大利润是580元；（3）或4．

【解析】

（1）设该加盟店的每天利润为元，先根据前20天的销售量和销售单价求出利润关于x的函数表达式，再利用二次函数的性质求解即可；

（2）同（1）的思路，先根据后20天的销售量和销售单价求出利润关于x的函数表达式，再利用一次函数的性质求解即可；

（3）先列出关于x的函数表达式，再根据“每一天的利润都不低于160元”列出不等式，从而可求出m的取值范围，由此即可得出答案．

设该加盟店的每天利润为元

（1）当时

由二次函数的性质可知，当时，随增大而增大；当时，随增大而减小

则当时，取得最大值，最大值为元

答：前20天中，第15天获得利润最大，最大利润是元；

（2）当时

因为

所以当时，随增大而减小

则当时，取得最大值，最大值为（元）

答：后20天中，第21天获得利润最大，最大利润是580元；

（3）由题意得：

，且为整数

由一次函数的性质可知，当时，随增大而减小

则当时，取得最小值，最小值为（元）

要使每一天的利润都不低于160元，则只需的最小值不低于160元即可

则

解得

因此，m的取值范围为且为整数

故m的值为3或4．