题目内容
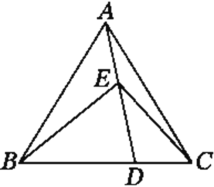
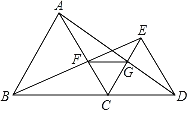
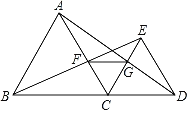
【题目】如图,B、C、D在同一直线上,△ABC和△CDE都是等边三角形,且在直线BD的同侧,连接BE交AC于点F,连接AD交CE于点G,连接FG.
(1)求证:AD=BE;
(2)求证:△ACG≌△BCF;
(3)试猜想△CFG的形状,并说明理由.
【答案】(1)见解析;(2)见解析;(3)△CFG是等边三角形,理由见解析.
【解析】
(1)根据△ABC和△CDE是等边三角形,得AC=BC,EC=CD,∠BCE=∠ACD,根据SAS得到△BEC≌△ADC,从而证得结论;
(2)由(1)中的结论△BEC≌△ADC,得∠CAG=∠CBF,结合等边三角形的性质,可证得结论;
(3)根据(2)的结论及∠FCG=60°,可推出△CFG是等边三角形.
(1)∵△ABC和△CDE是等边三角形,
∴BC =AC,EC=CD,∠ACB=∠ECD=60°,
∴∠BCE=∠ACD![]() .
.
在△BEC和△ADC中,
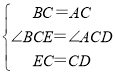 ,
,
∴△BEC≌△ADC(SAS),
∴BE=AD.
(2)∵△BCE≌△ACD(已证),
∴∠CAG=∠CBF
在△BCF和△ACG中,
 ,
,
∴△BCF≌△ACG(ASA),
(3)∵△BCF≌△ACG,
∴CF=CG.
又∵∠FCG=60°,
∴△CFG是等边三角形;

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目