��Ŀ����
����Ŀ���Ķ�������龰�Ի���Ȼ�������⣺
��ʦ�����Ƕ���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν�������������.
С�����ȱ�������һ��������������!
С������ֱ�����������Ƿ����������������?
����(1)���������������������Ķ��壬�����ж�С������IJ��룺���ȱ�������һ�����������������Ƿ���ȷ?__________.(����������������)
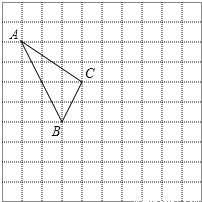
����(2)����֪Rt��ABC�У����߳��ֱ���![]() ��10��������������������������Σ����������__________.
��10������������������������������������__________.
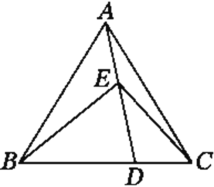
����(3)����ͼ����ABΪб�߷ֱ���AB��������ֱ�������Σ���AD=BD�����ı���ADBC�ڴ��ڵ�E��ʹ��AE=AD��CB=CE.��˵������ACE������������.

���𰸡���1���ǣ���2��5![]() ����3��������
����3��������
��������
���⣨1�������������������������εĶ���ֱ�ӽ����жϼ��ɣ�
���⣨2����c��б�ߺ�b��б������������ٸ��ݹ��ɶ����жϳ��������������Ƿ�������������εĶ��壮
���⣨3�����ù��ɶ�����AC2+BC2=AB2��AD2+BD2=AB2����AD=BD����AD=BD������2AD2=AB2������AE=AD��CB=CE������AC2+CE2=2AE2��Ȼ������¶��弴���ж���ACE�����������Σ�
��1���⣺��ȱ������ε�һ��Ϊa����a2+a2=2a2��
�������������������Ķ��壮
�ࡰ�ȱ�������һ������������������ȷ��
�ʴ�Ϊ���ǣ�
��2���⣺����10Ϊб��ʱ����һ��ֱ�DZ�=![]() =5
=5![]() ��
��
����![]() ��2+��
��2+��![]() ��2��2��102����
��2��2��102����![]() ��2+102��2����
��2+102��2����![]() ��2����
��2����
��Rt��ABC��������������
����![]() ��10��ֱ�DZ�ʱ��б��=
��10��ֱ�DZ�ʱ��б��=![]() =5
=5![]() ��
��
����![]() ��2+��5
��2+��5![]() ��2=200
��2=200
��2��102=200
����5![]() ��2+��5
��2+��5![]() ��2=2��102
��2=2��102
��Rt��ABC������������
�ʴ�Ϊ5![]() ��
��
��3��֤�����ߡ�ACB=��ADB=90����
��AC2+BC2=AB2��AD2+BD2=AB2��
��AD=BD��
��2AD2=AB2��
��AE=AD��CB=CE��
��AC2+CE2=2AE2��
���ACE������������