Question

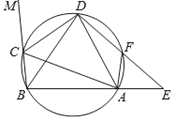
【题目】如图，在圆内接四边形ABCD中，CD为△BAC的外角平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．

（1）求证：AD=BD；

（2）若AC=10，AF=3，DF：FE=3：2，求DE的长．

Answer 1

【答案】（1）证明见解析；（2）5．

【解析】

（1）由圆内接四边形的性质以及圆的性质可求得∠DBA＝∠DAB，从而证明AD＝BD；

（2）由条件可证得△AEF∽△DAC，再利用相似三角形的性质可求得DE的长.

（1）证明：∵CD平分∠ACM，∴∠ACD=∠MCD，

∵四边形ABCD为圆内接四边形，∴∠MCD=∠BAD，

又∠ACD=∠ABD，∴∠BAD=∠ABD，∴AD=BD；

（2）解：∵BD=AD，BC=AF，∴=， =，

∴=，∴CD=DF，∵BC=AF，∴∠BDC=∠ADF，∴∠CDA=∠BDF=∠EAF，

由（1）可知∠DCA=∠DBA，且∠EFA=∠DBA，

∴∠DCA=∠EFA，∴△AEF∽△DAC，∴=，

∴=， =，∴EFDF=30，∵DF：FE=3：2，

∴设DF=3x，则FE=2x，∴6x2=30，解得x=，

∴DE=DF+FE=5x=5．