题目内容
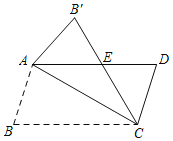
【题目】如图,ABCD中,AB=6,∠B=75°,将△ABC沿AC边折叠得到△AB′C,B′C交AD于E,∠B′AE=45°,则点A到BC的距离为( )
A.2![]() B.3
B.3![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过B′作B′H⊥AD于H,根据等腰直角三角形的性质得到AH=B′H=![]() AB′,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=75°,求得∠AEB′=60°,解直角三角形得到HE=
AB′,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=75°,求得∠AEB′=60°,解直角三角形得到HE=![]() B′H,B′E=2
B′H,B′E=2![]() ,根据平行线的性质得到∠DAC=∠ACB,推出AE=CE,根据全等三角形的性质得到DE=B′E=2
,根据平行线的性质得到∠DAC=∠ACB,推出AE=CE,根据全等三角形的性质得到DE=B′E=2![]() ,求得AD=AE+DE=3
,求得AD=AE+DE=3![]() +3
+3![]() ,过A作AG⊥BC于G,根据直角三角形的性质即可得到结论.
,过A作AG⊥BC于G,根据直角三角形的性质即可得到结论.
过B′作B′H⊥AD于H,
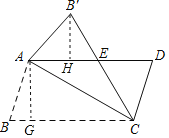
∵∠B′AE=45°,
∴△AB′H是等腰直角三角形,
∴AH=B′H=![]() AB′,
AB′,
∵将△ABC沿AC边折叠得到△AB′C,
∴AB′=AB=6,∠AB′E=∠B=75°,
∴∠AEB′=60°,
∴AH=B′H=![]() ×6=3
×6=3![]() ,
,
∴HE=![]() B′H=
B′H=![]() ,B′E=2
,B′E=2![]() ,
,
∵ABCD中,AD∥BC,
∴∠DAC=∠ACB,
∵∠ACB=∠ACB′,
∴∠EAC=∠ACE,
∴AE=CE,
∵∠AB′E=∠B=∠D,∠AEB′=∠CED,
∴△AB′E≌△CDE(AAS),
∴DE=B′E=2![]() ,
,
∴AD=AE+DE=3![]() +3
+3![]() ,
,
∵∠AEB′=∠EAC+∠ACE=60°,
∴∠ACE=∠CAE=30°,
∴∠BAC=75°,
∴AC=AD
过A作AG⊥BC于G,
∴AG=![]() AC=
AC=![]() ,
,
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目