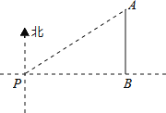Question

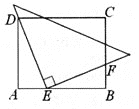
【题目】如图①，在我国古建筑的大门上常常悬挂着巨大的匾额，图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图．已知BC＝1米，∠MBC＝37°．从水平地面点D处看点C，仰角∠ADC＝45°，从点E处看点B，仰角∠AEB＝53°，且DE＝2.4米，求匾额悬挂的高度AB的长．（参考数据：sin37°≈，cos37°≈，tan37°≈）．

Answer 1

【答案】匾额悬挂的高度是4米．

【解析】

过C作CF⊥AM于F，过C作CH⊥AD于H，根据直角三角形的解法解答即可．

过C作CF⊥AM于F，过C作CH⊥AD于H，则四边形AHCF是矩形，所以AF＝CH，CF＝AH．

在Rt△BCF中，BC＝1，∠CBF＝37°．

BF＝BCcos37°＝0.8，CF＝BCsin37°＝0.6，

在Rt△BAE中，∠BEA＝53°，所以AE＝AB，

在Rt△CDH中，∠CDH＝45°，

∴CH＝DH＝FA＝0.8+AB，

∴AD＝AH+DH＝0.6+0.8+AB＝1.4+AB，

∵AD＝AE+DE＝AB+2.4，

∴1.4+AB＝AB+2.4，

AB＝4，

答：匾额悬挂的高度是4米．