题目内容
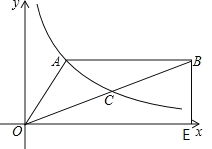
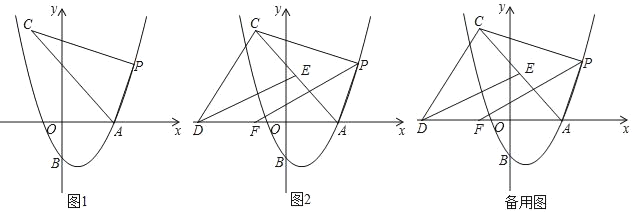
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
【答案】(1)![]() ;(2)①满足条件的t的值为2或﹣2+2
;(2)①满足条件的t的值为2或﹣2+2![]() 或﹣2﹣2
或﹣2﹣2![]() ;②综合以上可得t的值为
;②综合以上可得t的值为![]()
【解析】
(1)先根据直线解析式求出A、C两点的坐标,把点A和C点的坐标代入y=-![]() x2+bx+c得关于b和c的方程组,然后解方程组即可得到抛物线解析式;
x2+bx+c得关于b和c的方程组,然后解方程组即可得到抛物线解析式;
(2)当OC∥PM,且OC=PM时,以点C、O、M、P为顶点的四边形是平行四边形,可得关于t的方程,解方程即可;
(3)分三种情况考虑,当MP平分AC、MO的夹角,当AC平分MP、MO的夹角,当MO平分AC、MP的夹角,可由图形的性质得关于t的方程求解.
(1)在y=![]() x+3中,令x=0,y=3;令y=0,x=﹣4,得A(﹣4,0),C(0,3),
x+3中,令x=0,y=3;令y=0,x=﹣4,得A(﹣4,0),C(0,3),
代入抛物线y=-![]() x2+bx+c解析式得:
x2+bx+c解析式得: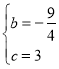 ,
,
∴抛物线的解析式![]() ;
;
(2)设P(t,![]() ),
),
∵四边形OCMP为平行四边形,
∴PM=OC=3,PM∥OC,
∴M点的坐标可表示为(t,![]() t+3),
t+3),
∴PM=![]() ,
,
∴|![]() =3,
=3,
当﹣![]() t2﹣3t=3,解得t=2,
t2﹣3t=3,解得t=2,
当﹣![]() t2﹣3t=﹣3,解得t1=﹣2+2
t2﹣3t=﹣3,解得t1=﹣2+2![]() ,t2=﹣2﹣2
,t2=﹣2﹣2![]() ,
,
综上所述,满足条件的t的值为2或﹣2+2![]() 或﹣2﹣2
或﹣2﹣2![]() ;
;
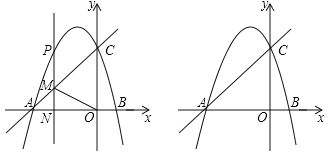
(3)如图1,

若当MP平分AC、MO的夹角,
则∠AMN=∠OMN,
∵PN⊥OA,
∴AN=ON,
∴t的值为﹣2;
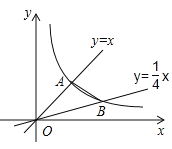
如图2,

若AC平分MP、MO的夹角,过点C作CH⊥OA,CG⊥MP,
则CG=CH,
∵![]() ,
,
∴OM=OC=3,
∵点M在直线AC上,
∴M(t,![]() t+3),
t+3),
∴MN2+ON2=OM2,可得,![]() ,
,
解得t=﹣![]() ,
,
如图3,
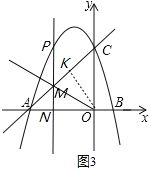
若MO平分AC、MP的夹角,则可得∠NMO=∠OMC,过点O作OK⊥AC,
∴OK=ON,
∵∠AKO=∠AOC=90°,∠OAK=OAC,
∴△AOK∽△ACO,
∴![]() ,
,
∴![]() ,
,
∴OK=![]() ,
,
∴t=﹣![]() ,
,
综合以上可得t的值为![]() .
.

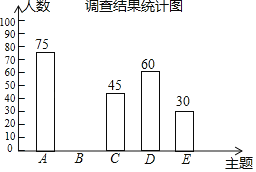
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.