题目内容
【题目】若一个三位数t＝
（其中a、b、c不全相等且都不为0），重新排列各数位上的数字必可得到一个最大数和一个最小数，此最大数和最小数的差叫做原数的差数，记为T（t）．例如，539的差数T（539）＝953﹣359＝594．
（1）根据以上方法求出T（268）＝ ，T（513）＝ ；
（2）已知三位数
（其中a＞b＞1）的差数T（）＝495，且各数位上的数字之和为3的倍数，求所有符合条件的三位数的值．
【答案】（1）594，396；（2）615，612
【解析】
（1）根据T（t）的求法，直接代入求解；(
)
（2）将T()用代数式表示为99a﹣99，确定a；再由a＞b＞1，确定b的可能取值，初步确定符合条件的三位数；最后结合各数位上的数字之和为3的倍数，准确得到符合条件的三位数．
（1）T（268）
；
T（513）
；
故答案为594，396；
（2）T()＝
，
∴
，
∵a＞b＞1，
∴b的可能值为5，4，3，2，
∴这个三位数可能是615，614，613，612，
∵各数位上的数字之和为3的倍数，
∴615，612满足条件，
∴符合条件的三位数的值为615，612．
阅读快车系列答案
【题目】山西省实验中学欲向清华大学推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人．投票结果统计如图1：
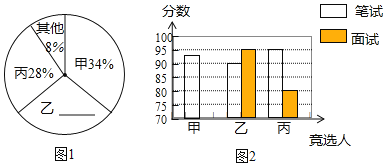
其次，对三名候选人进行了笔试和面试两项测试．各项成绩如表所示：
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图2是某同学根据上表绘制的一个不完全的条形图．请你根据以上信息解答下列问题：
（1）补全图1和图2；
（2）请计算每名候选人的得票数；
（3）若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？
（4）若学校决定从这三名候选人中随机选两名参加清华大学夏令营，求甲和乙被选中的概率．（要求列表或画树状图）
