题目内容
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,点
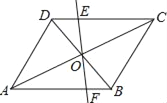
,点![]() 为
为![]() 上一个动点(不与
上一个动点(不与![]() ,
,![]() )重合),连接
)重合),连接![]() .
.


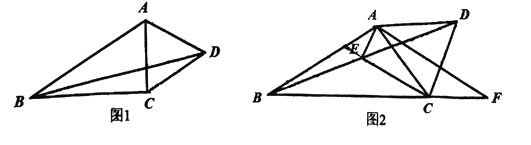
图1 图2
(1)直接写出![]() ___________,
___________,![]() ___________;
___________;
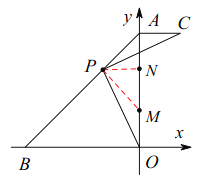
(2)如图1,过点![]() 作
作![]() 的垂线交过点
的垂线交过点![]() 平行于
平行于![]() 轴的直线于点
轴的直线于点![]() ,若点
,若点![]() ,
,
求点![]() 的坐标;
的坐标;
(3)如图2,以![]() 为斜边在
为斜边在![]() 右侧作等腰
右侧作等腰![]() ,
,![]() .连接
.连接![]() ,当点
,当点![]() 从
从![]() 向
向![]() 运动过程中,
运动过程中,![]() 的面积是否发生变化,请判断并说明理由.
的面积是否发生变化,请判断并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)面积不变为4,理由见解析.
;(3)面积不变为4,理由见解析.
【解析】
(1)根据完全平方公式即可化简,再根据非负性求解;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,证明△APM为等腰直角三角形,再得到
,证明△APM为等腰直角三角形,再得到![]() ,得到
,得到![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,根据
,根据![]() 得到
得到
![]() ,故可得到OM,即可求出AC的长,即可求解;
,故可得到OM,即可求出AC的长,即可求解;
(3)延长![]() 到
到![]() ,使
,使![]() , 得到
, 得到![]() 为等腰三角形,再证明
为等腰三角形,再证明![]() 得到
得到![]() ,根据直角三角形斜边上的中线性质得到AD=PD=DE,延长
,根据直角三角形斜边上的中线性质得到AD=PD=DE,延长![]() 至点
至点![]() ,使
,使![]() ,得到四边形APFE为矩形,得到点
,得到四边形APFE为矩形,得到点![]() 在运动过程中,点
在运动过程中,点![]() 在
在![]() 垂直平分线上运动,可得△BOD的BO边上的高为
垂直平分线上运动,可得△BOD的BO边上的高为![]() ,再根据三角形的面积即可求解.
,再根据三角形的面积即可求解.
(1)∵![]()
![]()
![]()
∴a+b=0,a-4=0,
∴a=4,b=-4
故答案为:![]() ,
,![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵A(0,4),B(-4,0)
∴∠BAO=45°,
∴△APM为等腰直角三角形,
∵∠OPC=∠MPA=90°
∴∠OPC-∠MPC=∠MPA-∠MPC
∴∠OPM=∠CPA
∴AP=MP,∠PAM=∠PMA=45°
又∠PAC=∠PMO=135°
∴![]() ,
,
![]() ,
,
过![]() 作
作![]() 轴于点
轴于点![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() ,
,
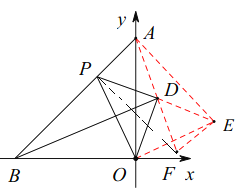
∵△POD为等腰直角三角形,
∴PD=OD=DE,OD⊥PE
则![]() 为等腰三角形,
为等腰三角形,
∴PO=EO
∴AO=BO,∠POE=∠AOB=90°,
∵∠POE-∠AOP=∠AOB-∠AOP
∴∠POB=∠EOA
∴![]() (SAS)
(SAS)
![]() ,
,
∴AD=PD=DE,
延长![]() 至点
至点![]() ,使
,使![]() ,
,
∴AD=DF=PD=DE,
∴四边形APFE为矩形,
![]() ,即
,即![]() ,
,
![]() 点
点![]() 在运动过程中,点
在运动过程中,点![]() 在
在![]() 垂直平分线上运动,
垂直平分线上运动,
∴△BOD的BO边上的高为![]() ,
,
![]() .
.

 阅读快车系列答案
阅读快车系列答案