题目内容
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() .
.
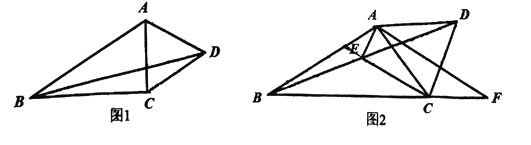
(1)如图1,若![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,且
,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使得
,使得![]() ,求证:
,求证:![]() ;
;
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)延长BC,作DE⊥BC,根据直角三角形的性质得出AC=2,BC=![]() ,然后根据等边三角形的性质即可得出△BCD的高,即可得出其面积;
,然后根据等边三角形的性质即可得出△BCD的高,即可得出其面积;
(2)延长AB到G使AG=AB,易△ADG△ACF,∠G=∠F=30°,AE是中位线,可得AE∥GD,得∠CFA=90°,AE=![]() DG=
DG=![]() CF,再证CH=
CF,再证CH=![]() CF,得CE=AH,可得四边形AECH是矩形,CE=AH,HF=
CF,得CE=AH,可得四边形AECH是矩形,CE=AH,HF=![]() AE即可.
AE即可.
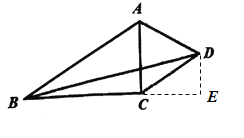
(1)延长BC,作DE⊥BC于点E,如图所示:
∵![]() ,
,![]()
∴AC=2,BC=![]()
又∵等边![]() ,DE⊥BC
,DE⊥BC
∴AC=CD=AD=2,∠DCE=30°
∴DE=1
∴![]()
故答案为![]() ;
;
(2)延长BA到G,使得AB=AG,连接DG,作CH⊥AF于H,如图所示:

∵![]() ,
,![]() ,AB=AG
,AB=AG
∴AB=AF=AG,∠BAF=120°
∴∠GAF=60°
∵等边![]()
∴∠CAD=60°,AC=AD,
∴∠CAF=∠DAG
∴△ACF≌△ADG(SAS)
∴DG=CF,∠AGD=∠AFC=30°
又∵点![]() 为
为![]() 中点,AB=AG,
中点,AB=AG,
∴![]() ,∠BAE=∠AGD=30°
,∠BAE=∠AGD=30°
∴∠EAF=90°
又∵CH⊥AF,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∵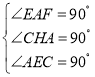
∴四边形AECH为矩形
∴AH=CE
∴![]()
即可得证.

练习册系列答案
相关题目