Question

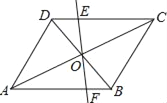
【题目】如图，点O是平行四边形ABCD的对称中心，将直线DB绕点O顺时针方向旋转，交DC、AB于点E、F．

（1）证明：△DEO≌△BFO；

（2）若DB=2，AD=1，AB=，当DB绕点O顺时针方向旋转45°时，判断四边形AECF的形状，并说明理由．

Answer 1

【答案】（1）证明见解析；（2）菱形，证明见解析.

【解析】

(1)由CD∥AB、OD=OB即可证明；

(2)由△DEO≌△BFO得OE=OF，结合OA=OC可判断AECF是平行四边形，再根据题干所给条件可证明∠AOE=90°，则可判定该四边形为菱形.

（1）证明：在平行四边形ABCD中，CD∥AB，

∴∠CDO=∠ABO，∠DEO=∠BFO．

又∵点O是平行四边形的对称中心，

∴OD=OB．

∴△DEO≌△BFO．

（2）解：∵在△ABD中，DB=2，AD=1，AB=，

∴DB2+AD2=AB2．

∴△ABD是直角三角形，且∠ADB=90°

∵OD=OB=DB=1，

∴AD=OD=1．

∴△OAD是等腰直角三角形，

∴∠AOD=45°．

当直线DB绕点O顺时针旋转45°时，即∠DOE=45°，

∴∠AOE=90°

∵△DEO≌△BFO，

∴OE=OF

又∵点O是平行四边形的对称中心，

∴OA=OC

∴四边形AECF是平行四边形

∴四边形AECF是菱形．