Question

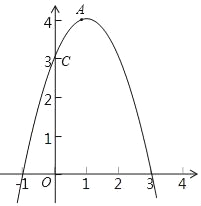
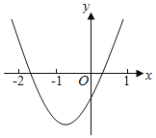
【题目】已知二次函数y＝ax2+bx+c(a≠0)图象如图所示，下列结论：①abc＜0；②2a﹣b＜0；③b2＞(a+c)2；④点(﹣3，y1)，(1，y2)都在抛物线上，则有y1＞y2．其中正确的结论有(　　)

A. 4个 B. 3个 C. 2个 D. 1个

Answer 1

【答案】B

【解析】

根据二次函数的性质逐一判断即可.

∵抛物线开口向上，

∴a>0，

∵对称轴x= <0，

∴b>0，

∵抛物线与y轴交点在y轴的下方，

∴c<0，

∴abc<0，故①正确.

∵对称轴x=>-1，

∴2a-b>0，故②错误，

∵x=-1时，a-b+c<0；x=1时，a+b+c>0；

∴（a-b+c）（a+b+c）<0

∴（a+c）2-b2<0，即b2>（a+c）2，故③正确，

观察图像可知：x=-3时抛物线上的点离对称轴远一些，x=1时抛物线上的点离对称轴近一些，所以y1>y2，故④正确，

综上所述：①③④正确共3个，

故选B