题目内容
【题目】如图,是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加( )m.

A. 1 B. 2 C. ![]() D.
D. ![]()
【答案】C
【解析】
根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=-1代入抛物线解析式得出水面宽度,即可得出答案.
建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,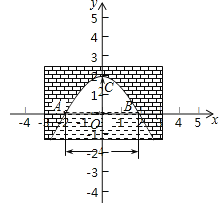
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(-2,0),
到抛物线解析式得出:a=-0.5,所以抛物线解析式为y=-0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=-1时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,
可以通过把y=-1代入抛物线解析式得出:
-1=-0.5x2+2,
解得:x=±![]() ,
,
所以水面宽度增加到2![]() 米,比原先的宽度当然是增加了2
米,比原先的宽度当然是增加了2![]() -4,
-4,
故选C..

练习册系列答案
相关题目
【题目】某公司欲将![]() 件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排
件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排![]() (
(![]() 为正整数)件产品运往甲地.
为正整数)件产品运往甲地.
(1)根据信息填表:
甲地 | 乙地 | 丙地 | |
产品件数(件) |
|
| |
运费(元) |
|
(2)若总运费为6300元,求![]() 与
与![]() 的函数关系式并求出
的函数关系式并求出![]() 的最小值.
的最小值.