题目内容
【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为( ![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 . 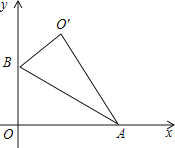
【答案】![]()
【解析】解:如图,作O′C⊥y轴于点C,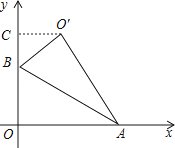
∵点A,B的坐标分别为( ![]() ,0),(0,1),∴OB=1,OA=
,0),(0,1),∴OB=1,OA= ![]() ,∴tan∠BAO=
,∴tan∠BAO= ![]() =
= ![]() ,
,
∴∠BAO=30°,
∴∠OBA=60°,
∵Rt△AOB沿着AB对折得到Rt△AO′B,
∴∠CBO′=60°,
∴设BC=x,则OC′= ![]() x,∴x2+(
x,∴x2+( ![]() x)2=1,解得:x=
x)2=1,解得:x= ![]() (负值舍去),∴OC=OB+BC=1+
(负值舍去),∴OC=OB+BC=1+ ![]() =
= ![]() ,∴点O′的坐标为(
,∴点O′的坐标为( ![]() ,
, ![]() ).
).
故答案为:( ![]() ,
, ![]() ).
).
作O′C⊥y轴于点C,首先根据点A,B的坐标分别为( ![]() ,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=
,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′= ![]() x,利用勾股定理求得x的值即可求解. 本题考查了翻折变换及坐标与图形的性质的知识,解题的关键是根据点A和点B的坐标确定三角形为特殊三角形,难度不大.
x,利用勾股定理求得x的值即可求解. 本题考查了翻折变换及坐标与图形的性质的知识,解题的关键是根据点A和点B的坐标确定三角形为特殊三角形,难度不大.

练习册系列答案
相关题目