Question

【题目】如图，在平面直角坐标系xOy中，△A′B′C′由△ABC绕点P旋转得到，则点P的坐标为 ．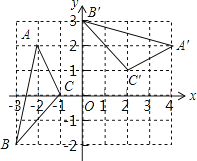

Answer 1

【答案】（1，﹣1）
【解析】解：连接AA′、CC′，
作线段AA′的垂直平分线MN，作线段CC′的垂直平分线EF，
直线MN和直线EF的交点为P，点P就是旋转中心．
∵直线MN为：x=1，设直线CC′为y=kx+b，
由题意： ，∴ ，∴直线CC′为y= x+ ，∵直线EF⊥CC′，经过CC′中点（ ， ），
∴直线EF为y=﹣3x+2，
由 得 ，
∴P（1，﹣1）．
故答案为（1，﹣1）．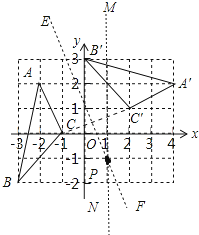

连接AA′，CC′，线段AA′、CC′的垂直平分线的交点就是点P． 本题考查旋转的性质，掌握对应点连线段的垂直平分线的交点就是旋转中心，是解题的关键．