题目内容
【题目】请阅读下列材料,并完成相应的任务。
阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.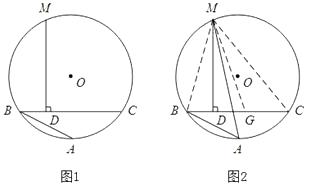
阿基米德折弦定理:如图1,AB和BC是圆O的两条弦(即折线ABC是圆的一条折弦), BC>AB,M是 ![]() 的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
证明:如图2,在CB上截取CG=AB,连接MA、MB、MC、MG。因为M是弧ABC的中点,所以MA=MC.
任务:
(1)请按照上面的证明思路,完整证明阿基米德折弦定理,即CD=AB+BD。
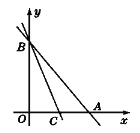
(2)如图3,已知等边△ABC内接于圆O,AB=1,D为 ![]() 上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
![]()
【答案】
(1)
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG;
∵M是狐ABC的中点,
∴MA=MC.
在△MBA和△MGC中,
∵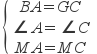
∴△MBA≌△MGC(SAS),
∴MB=MG,
又∵MD⊥BC,
∴BD=GD
∴DC=GC+GD=AB+BD
(2)解:如图3,截取BF=CD,连接AF,AD,CD;
根据题意可得:AB=AC,∠ABF=∠ACD,
在△ABF和△ACD中
∵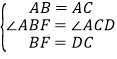
∴△ABF≌△ACD(SAS)
∴AF=AD
∵AE⊥BD
∴FE=DE,则CD+DE=BE
∵∠ABD=45°
∴BE=![]() =
=![]() ,
,
则C△BDC=![]() +1
+1
因此,本题正确答案是![]() +1
+1
【解析】(1)首先证明△MBA≌△MGC(SAS),进而得出MB=MG,再利用等腰三角形的性质得出BD=GD,即可得出答案;
(2)首先证明△ABF≌△ACD(SAS),进而得出AF=AD,以及CD+DE=BE,进而求出DE的长即可得出答案。
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案