题目内容
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.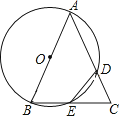
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
【答案】
(1)
证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC
(2)
解:连接AE,
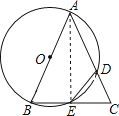
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE= ![]() BC=
BC= ![]() ,
,
∵CECB=CDCA,AC=AB=4,
∴ ![]() 2
2 ![]() =4CD,
=4CD,
∴CD= ![]()
【解析】(1)由等腰三角形的性质得到∠EDC=∠C,由圆外接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,由“三线合一”定理得到BE=CE= ![]() BC=
BC= ![]() ,由割线定理可证得结论.本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.
,由割线定理可证得结论.本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目