题目内容
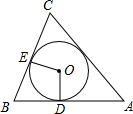
如图，⊙O是△ABC的内切圆，D，E，F是切点，∠A=50°，∠C=60°，则∠DOE=（ ）
| A．70° | B．110° | C．120° | D．130° |
∵∠BAC=50°，∠ACB=60°，∴∠B=180°-50°-60°=70°，
∵E，F是切点，
∴∠BDO=∠BEO=90°，
∴∠DOE=180°-∠B，∴∠DOE=∠A+∠C=50°+60°=110°．
故选：B．
∵E，F是切点，
∴∠BDO=∠BEO=90°，
∴∠DOE=180°-∠B，∴∠DOE=∠A+∠C=50°+60°=110°．
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
