题目内容
已知：如图，四边形ABCD中，对角线AC⊥BD于O，AC=24，BD=10，点E、F、G分别为AB、BC、CD的中点．试求点E、F、G三点所确定的圆的周长．（结果保留π）
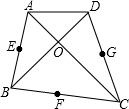
连接EF、FG、EG；
∵E、F分别是AB、BC的中点，
∴EF是△ABC的中位线，
∴EF∥AC，且EF=
AC=12；
同理可得：FG∥BD，且FG=
BD=5；
由于AC⊥BD，则EF⊥FG；
在Rt△EFG中，EF=12，FG=5，则EG=13；
由于直角三角形的外接圆直径等于斜边的长，
∴点E、F、G三点所确定的圆的周长为：13π．
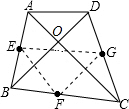
∵E、F分别是AB、BC的中点，
∴EF是△ABC的中位线，
∴EF∥AC，且EF=
| 1 |
| 2 |
同理可得：FG∥BD，且FG=
| 1 |
| 2 |
由于AC⊥BD，则EF⊥FG；
在Rt△EFG中，EF=12，FG=5，则EG=13；
由于直角三角形的外接圆直径等于斜边的长，
∴点E、F、G三点所确定的圆的周长为：13π．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
