题目内容
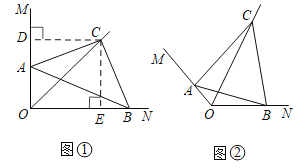
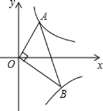
【题目】如图，已知点A、B分别在反比例函数
，
的图象上，且OA
OB， 则
的值为 ____________ ．
【答案】
【解析】
过点A作AM⊥y轴于点M，过点B作BN⊥y轴于点N，利用相似三角形的判定定理得出△AOM∽△OBN，再由反比例函数系数k的几何意义得出S△AOM：S△BON=1:2，进而可得出结论．
解：过点A作AM⊥y轴于点M，过点B作BN⊥y轴于点N，
∴∠AMO=∠BNO=90°，
∴∠AOM+∠OAM=90°，
∵OA⊥OB，
∴∠AOM+∠BON=90°，
∴∠OAM=∠BON，
∴△AOM∽△OBN，
∵点A，B分别在反比例函数
，
的图象上，
∴S△AOM：S△BON=2:4=1:2，
∴AO:BO=1:
，
∴OB:OA=．
故答案为：.
练习册系列答案
相关题目
【题目】4月23日是世界读书日，某校为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：
数据收集：从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下(单位：
)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据：按如下分段整理样本数据并补全表格：
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
分析数据：补全下列表格中的统计量：
平均数 | 中位数 | 众数 |
80 |
|
|
（1）
，
，
，
；
（2）用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ；
（3）如果该校现有学生400人，估计等级为“
”的学生有多少名？
