题目内容
【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.
【答案】(1)190,67500;(2)![]() ,
,![]() ;(3)7500,60.
;(3)7500,60.
【解析】
(1)设![]() ,把x=1500,y=185;x=2000,y=180,代入
,把x=1500,y=185;x=2000,y=180,代入![]() ,得到关于k,b的二元一次方程组,求出k,b的值即可,再根据
,得到关于k,b的二元一次方程组,求出k,b的值即可,再根据![]() ,求出
,求出![]() 的解析式,分别求出当x=1000时,
的解析式,分别求出当x=1000时,![]() ,
,![]() 的值即可;
的值即可;
(2)根据“利润=销售额-成本-广告费”和“利润=销售额-成本-附加费”,分别求出![]() 、
、![]() 与
与![]() 的函数关系式即可;
的函数关系式即可;
(3)根据二次函数图象的顶点坐标公式,即可求得![]() 最大时,所对应的x的值,然后根据题意列出关于a的方程,即可求解.
最大时,所对应的x的值,然后根据题意列出关于a的方程,即可求解.
(1)设![]() ,
,
由题意得:![]() ,解得
,解得 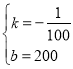 ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() ,
,
∵ ![]()
∴当![]() 时,
时,![]() ,
,
故答案是:190,67500;
(2)由题意得:![]() ,
,
![]() .
.
(3)∵![]()
∴当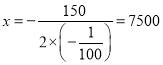 时,
时,![]() 最大.
最大.
由题意得: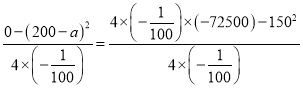 ,解得
,解得![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目