题目内容
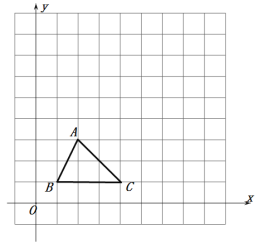
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,

(1)图1中共有_______对相似三角形;
(2)已知![]() ,请求出
,请求出![]() 的长;
的长;
(3)在(2)的情况下,如果以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,点
轴,点![]() 为坐标原点
为坐标原点![]() ,建立直角坐标系(如图2),若点
,建立直角坐标系(如图2),若点![]() 从
从![]() 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段![]() 运动,点
运动,点![]() 出
出![]() 点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动:设运动时间为
点出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动:设运动时间为![]() 秒是否存在点
秒是否存在点![]() ,使以点
,使以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;(2)4.8;(3)点P的坐标为(1.35,3)或(3.15,1.8).
【解析】
(1)根据直角三角形性质和相似三角形判定可得结果;(2)根据勾股定理和三角形面积公式可得;(3)分类讨论:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB;②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB;根据相似三角形性质和勾股定理可得.
(1)根据已知可得:∠A=∠BCD, ∠B=∠ACD,故:图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,
∴BC=![]() =6.
=6.
∵△ABC的面积=![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=![]() =4.8;
=4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:
在△BOC中,∵∠COB=90°,BC=6,OC=4.8,
∴OB=![]() =3.6.
=3.6.
分两种情况:
①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
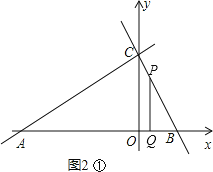
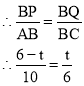
解得t=2.25,即BQ=CP=2.25,
∴OQ=OB-BQ=3.6-2.25=1.35,BP=BC-CP=6-2.25=3.75.
在△BPQ中,由勾股定理,得PQ=![]() =
=![]() =3,
=3,
∴点P的坐标为(1.35,3);
②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,
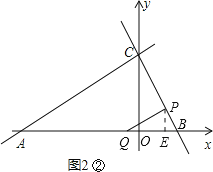
∴![]()
![]() ∴
∴![]() ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC-CP=6-3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,
∴![]() ,即
,即![]() ,
,
∴PE=1.8.
在△BPE中,BE=![]() =0.45,
=0.45,
∴OE=OB-BE=3.6-0.45=3.15,
∴点P的坐标为(3.15,1.8);
综上可得,点P的坐标为(1.35,3)或(3.15,1.8).

【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.