题目内容
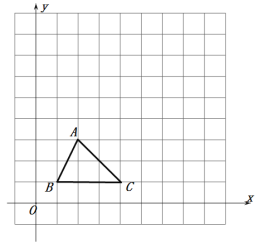
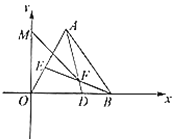
【题目】如图,在平面直角坐标系中,等边![]() 的边
的边![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() ,
,![]() ,点
,点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 出发以相同的速度向
出发以相同的速度向![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() 交于点
交于点![]() ,
,![]() 是
是![]() 轴上一点,则
轴上一点,则![]() 的最小值为______.
的最小值为______.
【答案】![]()
【解析】
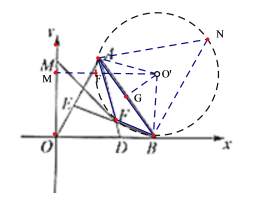
先证明![]() ,即可得出∠AFB=120°,即可判断出点F的轨迹是以O’为圆心的圆上的一段弧(劣弧AB),然后确定出圆心O’的位置及其坐标,即可确定点M和点F的位置,使FM的长度最小.
,即可得出∠AFB=120°,即可判断出点F的轨迹是以O’为圆心的圆上的一段弧(劣弧AB),然后确定出圆心O’的位置及其坐标,即可确定点M和点F的位置,使FM的长度最小.
如图,∵![]() 是等边三角形,
是等边三角形,
∴∠AOB=∠ABD=60°,OB=AB,
∵点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 出发以相同的速度向
出发以相同的速度向![]() 、
、![]() 运动,
运动,
∴BD=OE,
在OBE和DAB中,
∵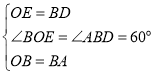
∴![]() ,
,
∴∠OBE=∠BAD,
∴∠ABE+∠BAD= ∠ABE+∠OBE=∠ABO=60°,
∴∠AFB=180°-(∠ABE+∠BAD)=120°,
∴点F是经过点A,B,F的圆上的点,记圆心为O’,在圆O’上取一点N,使
点N和点F在弦AB的两侧,连接AN,BN,
∴∠ANB=180°-∠AFB=60°,
连接O’A,O’B,
∴∠AO’B=2∠ANB=120°,
∵O’A=O’B,
∴∠ABO’=∠BAO’,
∴∠ABO’=![]() (180°-∠AO’B)=
(180°-∠AO’B)=![]() (180°-120°)=30°,
(180°-120°)=30°,
∵∠ABO=60°,
∴∠OBO’=90°,
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴AB=OB=2×3=6,a=![]() ,
,
过点O’作O’G⊥AB,
∴BG=![]() AB=3,
AB=3,
在RtBO’G中,∠ABO’=30°,BG=3,
∴O’B=![]() ,
,
∴![]() ),
),
∵![]() 的最小值= O’M最小值- O’F,
的最小值= O’M最小值- O’F,
∴过点O’作O’M⊥y轴,垂足为M,则四边形O’MOB是矩形,此时,O’M长度最小,最小值为6,O’M与圆O’的交点,即为点F的位置,
∵O’F=O’B=![]() ,
,
∴![]() 的最小值= O’M最小值- O’F=6-
的最小值= O’M最小值- O’F=6-![]() .
.
故答案是:![]() .
.

【题目】某公司生产一种节能型灯具并加以销售,现准备在甲市和乙市按不同的方案进行销售,若只在甲市销售,销售价为![]() (元/件),月销售量为
(元/件),月销售量为![]() (件),
(件),![]() 是
是![]() 的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为
的一次函数.如表所示,成本为50元/件,无论销售多少,每月还需支出广告费用72500元。设月利润为![]() (元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为
(元),(利润=销售额-成本-广告费).若只在乙市销售,销售价为200元/件,受各种因素影响,成本为![]() 元/件(
元/件(![]() 为常数且
为常数且![]() ),当月销售量为
),当月销售量为![]() 件时,每月还需交纳
件时,每月还需交纳![]() 的附加费,设月利润为
的附加费,设月利润为![]() (元).(利润=销售额-成本-附加费)
(元).(利润=销售额-成本-附加费)
月销售量 | 1500 | 2000 |
销售价格 | 185 | 180 |
(1)当![]() 时,
时,![]() ______元/件,
______元/件,![]() ______元(直接写出结果).
______元(直接写出结果).
(2)分别求出![]() 、
、![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的取值范围).
的取值范围).
(3)当![]() 为何值时,
为何值时,![]() 最大?若在乙市销售月利润最大值与甲市最大值相同,求
最大?若在乙市销售月利润最大值与甲市最大值相同,求![]() 的值.
的值.