Question

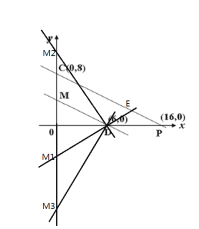
【题目】如图，四边形OABC是一张放在平面直角坐标系中的矩形纸片，点A在x轴上，点C在y轴上，将边BC折叠，使点B落在OA上的点D处，已知折痕CE=5,且4AE=3AD.

①判断△OCD与△ADE是否相似，请说明理由。

②求直线CE与x轴的交点P的坐标。

③是否存在过点D的直线l，使直线l与两坐标轴围成的三角形与直线CE与两坐标轴围成的三角形相似，如果存在，请求出其解析式，如果不存在，请说明理由。

Answer 1

【答案】①相似，证明详见解析；②P（16，0）；③存在，;;y=-2x+12;

【解析】

（1）运用同角的余角相等得到∠CDO=∠DEA即可证明相似,

（2）由△OCD∽△ADE求出OA,OD之间的关系,再在直角三角形CBE中勾股定理即可解题,

（3）分情况讨论,当△ODM∽△OPC时和当△OMD∽△OPC由比例式得到M的坐标即可求解.

解：①由对称性得∠CDE=∠B=90°

∴∠CDO+∠EDA=90°

∴∠CDO=∠DEA

∵∠COD=∠DAE=90°

∴△OCD∽△ADE

②设AE=3x

∵tan∠EDA=

∴AD=4x,DE=5x

∴AB=8x=OC

∵由△OCD∽△ADE

∴

∴OD=6x

∴OA=10x

∵CE2=CB2+BE2

∴（5）2=（10x）2+（5x）2

∴x=1

∴OA=10=CB，OC=AB=8，AE=3

∴C（0，8） E（10，3） D（6，0）

设直线CE的解析式为y=kx+b

∴

∴

∴，

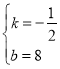
令y=0,解得：x=16,

∴与x轴交点P的坐标是（16，0）

③存在,

当DM∥CP时

△ODM∽△OPC

∴

∴OM=3

∴M（0，3）

∴

由对称性 M1（0，-3）

∴

当∠OMD=∠OPC时

△OMD∽△OPC

∴

∴OM=12

∴M2（0，12）

∴y=-2x+12

由对称性M3（0，-12）

∴