题目内容
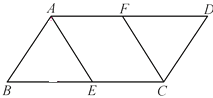
【题目】如图，在ABCD中，BC＝2AB＝4，点E，F分别是BC，AD的中点．
(1)求证：△ABE≌△CDF；
(2)当四边形AECF为菱形时，求出该菱形的面积．
【答案】见试题解析
【解析】
试题（1）由□ABCD可得AB=CD，BC=AD，∠ABC=∠CDA，再结合点E、F分别是BC、AD的中点即可证得结论；
（2）当四边形AECF为菱形时，可得△ABE为等边三角形，根据等边三角形的性质即可求得结果。
∵在□ABCD中，AB=CD，
∴BC=AD，∠ABC=∠CDA．
又∵BE=EC=
BC，AF=DF=AD，
∴BE=DF．
∴△ABE≌△CDF．
（2）当四边形AECF为菱形时，△ABE为等边三角形，
四边形ABCD的高为
,
∴菱形AECF的面积为2.
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
【题目】茶叶是安徽省主要经济作物之一，2020年新茶上市期间，某茶厂为获得最大利益，根据市场行情，把新茶价格定为400元/kg，并根据历年的相关数据整理出第x天（1≤x≤15，且x为整数）制茶成本（含采摘和加工）和制茶量的相关信息如下表．假定该茶厂每天制作和销售的新茶没有损失，且能在当天全部售出（当天收入=日销售额-日制茶成本）
制茶成本（元/kg） | 150+10x |
制茶量（kg） | 40+4x |
（1）求出该茶厂第10天的收入；
（2）设该茶厂第x天的收入为y（元）．试求出y与x之间的函数关系式，并求出y的最大值及此时x的值．
