题目内容
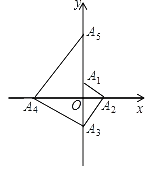
【题目】如图,已知点A1的坐标为(0,1),点A2在x轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,交y轴于点A3;过点A3作A3A4⊥A2A3,交x轴于点A4;过点A4作A4A5⊥A3A4,交y轴于点A5;……;按此规律进行下去,则点A2021的坐标为( )
A.(0,31011)B.(﹣31011,0)C.(0,31010)D.(﹣31010,0)
【答案】C
【解析】
通过解直角三角形可得出点A2的坐标,同理可得出点A3,A4,A5,A6,A7,…的坐标,根据坐标的变化可得出变化规律“点A4n+1的坐标为(0,32n)(n为正整数)”,再结合2021=505×4+1即可得出点A2021的坐标,此题得解.
解:∵∠A1A2O=30°,OA1=1,
∴OA2=![]() ,
,
∴点A2的坐标为(![]() ,0),
,0),
同理,A3(0,﹣3,),A4(﹣3![]() ,0),A5(0,9),A6(9
,0),A5(0,9),A6(9![]() ,0),A7(0,﹣27),…,
,0),A7(0,﹣27),…,
∴点A4n+1的坐标为(0,32n)(n为正整数).
∵2021=505×4+1,
∴点A2021的坐标为(0,31010).
故选:C.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】2020年春节,一场突如其来的新型冠状肺炎病毒疫情在武汉突发,为响应党中央号召,在“支援武汉,防控疫情”的过程中,某省计划组织1441名医护人员的“援汉”团队前往武汉进行支援,经过研究,决定租用当地租车公司一共62辆![]() 、
、![]() 两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 380元 |
| 20人 | 280元 |
注:载客量指的是每辆客车最多可载医护人员的人数.
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过19900元,一共有几种租车方案?哪种租车方案最省钱?