题目内容
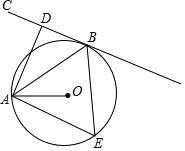
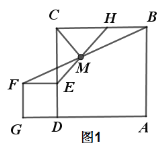
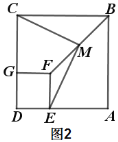
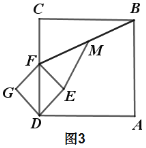
【题目】如图,正方形ABCD的边长为6,点E是BC的中点,连接AE与对角线BD交于点G,连接CG并延长,交AB于点F,连接DE交CF于点H,连接AH.以下结论:①CF⊥DE;②![]() ;③AD=AH;④GH=
;③AD=AH;④GH=![]() ,其中正确结论的序号是__________.
,其中正确结论的序号是__________.
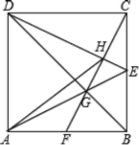
【答案】①②③④
【解析】
根据全等三角形的判定定理证出![]() 和
和![]() ,根据全等三角形的性质证出∠CDE=∠BCF,即可证出∠CHE=90°,从而判断①;根据勾股定理求出DE,利用面积求出CH,证出
,根据全等三角形的性质证出∠CDE=∠BCF,即可证出∠CHE=90°,从而判断①;根据勾股定理求出DE,利用面积求出CH,证出![]() ,即可求出HF,从而判断②;过点A作AM⊥DH于M,证出AM垂直平分DH,即可判断③;证出
,即可求出HF,从而判断②;过点A作AM⊥DH于M,证出AM垂直平分DH,即可判断③;证出![]() ,列出比例式即可判断④.
,列出比例式即可判断④.
解:∵正方形ABCD的边长为6,点E是BC的中点,BD为正方形的对角线
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
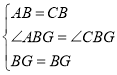
∴![]()
∴![]()
∴∠CDE=∠BCF
∵∠CDE+∠CED=90°
∴∠BCF+∠CED=90°
∴∠CHE=90°
∴CF⊥DE,故①正确;
∵![]() ,
,
根据勾股定理![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴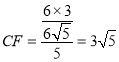
∴HF=CF-CH=![]()
∴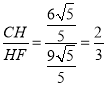 ,故②正确;
,故②正确;
过点A作AM⊥DH于M

∵![]()
根据勾股定理可得![]()
∵![]()
∴![]()
∵CD=DA,∠DHC=∠AMD=90°
∴![]()
∴DM=![]() ,
,![]()
∴DM=![]() ,
,
∴AM垂直平分DH
∴AD=AH,故③正确;
∵![]()
∴EH=DE-DH=![]() ,
,![]()
∵![]()
∴AM∥CF
∴![]()
∴![]()
即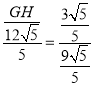
解得GH=![]() ,故④正确.
,故④正确.
综上:正确的有①②③④.
故答案为:①②③④.

练习册系列答案
相关题目