题目内容
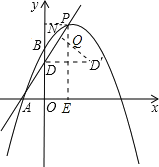
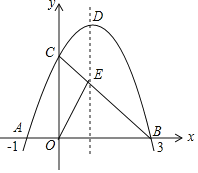
【题目】如图，已知二次函数
的图象与x轴负半轴交于点A（-1，0），与y轴正半轴交与点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．
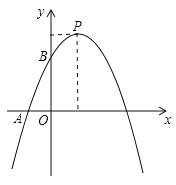
(1) 求一次函数解析式；
(2)求顶点P的坐标；
(3)平移直线AB使其过点P，如果点Ｍ在平移后的直线上，且
，求点M坐标；
(4)设抛物线的对称轴交x轴与点E，联结AP交y轴与点D，若点Q、N分别为两线段PE、PD上的动点，联结QD、QN，请直接写出QD+QN的最小值．
【答案】(1) 一次函数的解析式为：y=3x+3
(2)顶点P的坐标为（1，4）
(3) M点的坐标为：
）
（4）最小值为
【解析】
（1）根据抛物线的解析式即可得出B（0，3），根据OB=3OA，可求出OA的长，也就得出了A点的坐标，然后将A、B的坐标代入直线AB的解析式中，即可得出所求；
（2）将（1）得出的A点坐标代入抛物线的解析式中，可求出a的值，也就确定了抛物线的解析式进而可求出P点的坐标；
（3）易求出平移后的直线的解析式，可根据此解析式设出M点坐标（设横坐标，根据直线的解析式表示出纵坐标）．然后过M作x轴的垂线设垂足为E，在构建的直角三角形AME中，可用M点的坐标表示出ME和AE的长，然后根据∠OAM的正切值求出M的坐标．（本题要分M在x轴上方和x轴下方两种情况求解．方法一样．）
（4）作点D关于直线x=1的对称点D′，过点D′作D′N⊥PD于点N，根据垂线段最短求出QD+QN的最小值．
(1)∵A（-1，0）,∴OA=1
∵OB=3OA，∴B（0，3）
∴图象过A、B两点的一次函数的解析式为：y=3x+3
(2)∵二次函数
的图象与x轴负半轴交与点A（-1，0），与y轴正半轴交与点B（0，3），
∴c=3,a=-1
∴二次函数的解析式为：
∴抛物线的顶点P（1，4）
(3)设平移后的直线的解析式为：
∵直线过P（1，4）
∴b=1
∴平移后的直线为
∵M在直线，且
设M（x,3x+1）
① 当点M在x轴上方时，有
，∴
∴
②当点M在x轴下方时，有
，∴
∴
）
(4)作点D关于直线x=1的对称点D’，过点D’作D’N⊥PD于点N
当-x2+2x+3=0时，解得，x=-1或x=3，
∴A（-1，0），
P点坐标为（1，4），
则可得PD解析式为：y=2x+2，
令x=0，可得y=2，
∴D（0，2），
∵D与D′关于直线x=1对称，
∴D′（2，2）．
根据ND′⊥PD，
设ND′解析式为y=kx+b，
则k=-
，即y=-x+b，
将D′（2，2）代入，得2=-×2+b，解得b=3，
可得函数解析式为y=-x+3，
将两函数解析式组成方程组得：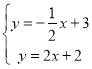
，
解得
，
故N（
，
由两点间的距离公式：d=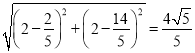
，
∴所求最小值为
