题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一个动点,将四边形
边上的一个动点,将四边形![]() 沿直线
沿直线![]() 折叠,得到四边形
折叠,得到四边形![]() ,点
,点![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() .直线
.直线![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,已知
,已知![]() .
.
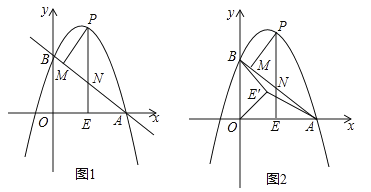
①如图①,当![]() ,
,![]() 时,求
时,求![]() 的长度;
的长度;
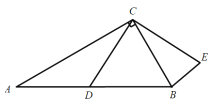
②如图②,当四边形![]() 为菱形时,请直接写出
为菱形时,请直接写出![]() 的长度.
的长度.
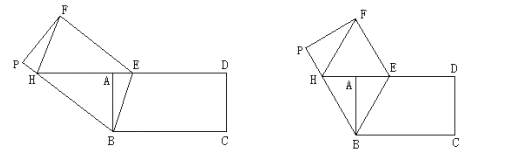
图① 图②
【答案】(1)证明见解析;(2)①![]() ,②3
,②3![]() .
.
【解析】
(1)根据折叠的性质和平行线的性质得:![]() ,则
,则![]() ;
;
(2)先在Rt△BAH中根据勾股定理列方程计算![]() 的长,进而求出PH,再在Rt△PFH中求出FH即可;
的长,进而求出PH,再在Rt△PFH中求出FH即可;
(3)由四边形![]() 为菱形结合(1)
为菱形结合(1)![]() ;可知△BEH为等边三角形,结合30°三角形性质可得BE=
;可知△BEH为等边三角形,结合30°三角形性质可得BE=![]() ,进而根据折叠性质求出AD.
,进而根据折叠性质求出AD.
(1)证明:在矩形ABCD中,AD∥BC,
由将四边形BCDE沿直线BE折叠,得到四边形BEFG,
得,∠HBE=∠CBE,
∴∠HEB=∠CBE,
∴∠HBE=∠HEB,
∴EH=BH
(2)①∵AD=6,AE=![]() AD,
AD,
∴AE=1,
∵EH=BH,
∴AH=EH-AH=BH-1
又在矩形ABCD中,∠BAD=90°,
∴∠BAH=90°.
在Rt△BAH中,![]() ,
,
∴![]() ,
,
∴![]() .
.
由将四边形BCDE沿直线BE折叠,得到四边形BEFP,
得,BP=BC=AD=6,PF=CD=3,∠FPH=90°
∴![]() ,
,
在Rt△PFH中,![]() .
.
②AD=3![]() .
.
理由如下:由将四边形BCDE沿直线BE折叠,得到四边形BEFP,可知 ED=EF,
当四边形![]() 为菱形时,则BH=BE=EF,
为菱形时,则BH=BE=EF,
由(1)可知,EH=BH,
∴△BEH为等边三角形,
∴∠ABE=60°,
∵∠EAB=90°,![]() ,
,
∴![]() ,
,![]() ,
,
∵AD=AE+ED,ED=EF,
∴![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】 某射击队教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如表:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
关于以上数据,下列说法错误的是( )
A.甲命中环数的中位数是8环
B.乙命中环数的众数是9环
C.甲的平均数和乙的平均数相等
D.甲的方差小于乙的方差