题目内容
【题目】如图,A(2,0),D(6,4),将线段AD平移得到BC,B(0,﹣6),延长BC交x轴于点E.
(1)则△ABC的面积是 ;
(2)Q为x轴上一动点,当△ABC与△ADQ的面积相等时,试求点Q的坐标.
(3)若存在一点M(m,6)且△ADM的面积不小于△ABC的面积,求m的取值范围.

【答案】(1)△ABC的面积为8;(2)当△ABC与△ADQ的面积相等时,点Q的坐标为(﹣2,0)或(6,0);(3)△ADM的面积不小于△ABC的面积,m的取值范围为m≤4或m≥12.
【解析】
(1)连接AC作CH⊥AE于H,根据平移的性质求出点C的坐标,根据梯形的面积公式、三角形的面积公式计算即可;
(2)设点Q的坐标为(x,0),根据题意列出方程,解方程即可;
(3)直线BC的解析式为y=x-6,直线y=x-6交直线y=6于M′(12,6),此时△ADM′的面积=8,由A(2,0),D(6,4),推出直线AD的解析式为y=x-2,直线y=x-2交y轴于P(0,-2),在y轴上取一点N,使得PN=PB,则N(0,2),作NM∥AD,直线MN的解析式为y=x+2,直线MN交直线y=6于M(4,6),此时△ADM的面积=8,由此几何图形即可解决问题.
(1)如图1中,连接AC作CH⊥AE于H,

∵点A的坐标为(2,0),点B的坐标为(0,﹣6),
∴点A先向左移动2个单位,再向下移动6个单位得到点B,
∵点D的坐标为(6,4),
∴点C的坐标为(4,﹣2),
∴△ABC的面积=![]() ×(2+6)×4﹣
×(2+6)×4﹣![]() ×2×6﹣
×2×6﹣![]() ×2×2=8,
×2×2=8,
故答案为:8;
(2)设点Q的坐标为(x,0)
由题意得,![]() ×|x﹣2|×4=8,
×|x﹣2|×4=8,
解得,x=﹣2或6,
∴当△ABC与△ADQ的面积相等时,点Q的坐标为(﹣2,0)或(6,0);
(3)如图2中,
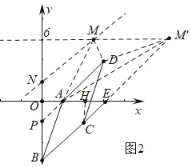
∵B(0,﹣6),C(4,﹣2),
∴直线BC的解析式为y=x﹣6,直线y=x﹣6交直线y=6于M′(12,6),此时△ADM′的面积=8,
∵A(2,0),D(6,4),
∴直线AD的解析式为y=x﹣2,直线y=x﹣2交y轴于P(0,﹣2),
在y轴上取一点N,使得PN=PB,则N(0,2),作NM∥AD,
直线MN的解析式为y=x+2,直线MN交直线y=6于M(4,6),此时△ADM的面积=8,
∴△ADM的面积不小于△ABC的面积,m的取值范围为m≤4或m≥12.