��Ŀ����
����Ŀ��������һ�����⣺̽��ͬһƽ��ֱ������ϵ��ϵ����Ϊ��������������������y= ![]() x��y=
x��y= ![]() ��k��0����ͼ�����ʣ�
��k��0����ͼ�����ʣ�
С������ѧϰ�����ľ��飬�Ժ���y= ![]() x��y=
x��y= ![]() ����k��0ʱ��ͼ�����ʽ�����̽����
����k��0ʱ��ͼ�����ʽ�����̽����
������С����̽�����̣�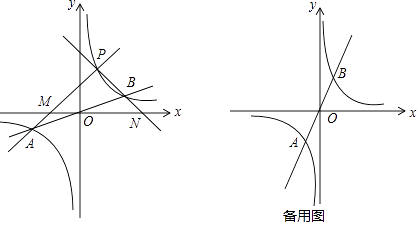
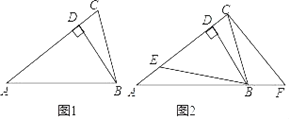
��1����ͼ��ʾ���躯��y= ![]() x��y=
x��y= ![]() ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ��
ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ��
��2������PΪ��һ������˫�����ϲ�ͬ�ڵ�B������һ�㣮
����ֱ��PA��x���ڵ�M��ֱ��PB��x���ڵ�N����֤��PM=PN��
֤���������£���P��m�� ![]() ����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
�� 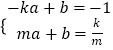 ��
��
��� ![]()
��ֱ��PA�Ľ���ʽΪ ![]()
���������Ľ����̲��������������ʣ���֤����
�ڵ�P������Ϊ��1��k����k��1��ʱ���жϡ�PAB����״������k��ʾ����PAB�������
���𰸡�
��1����k��1��
��2��
�ڽ⣺�ɢٿ�֪���ڡ�PMN�У�PM=PN��
���PMN������������MH=HN=k��
��P������Ϊ��1��k��ʱ��PH=k��
��MH=HN=PH��
���PMH=��MPH=45�㣬��PNH=��NPH=45�㣬
���MPN=90�㣬����APB=90�㣬
���PABΪֱ�������Σ�
��k��1ʱ����ͼ1��
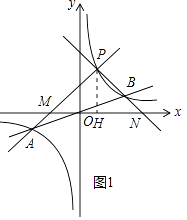
S��PAB=S��PMN��S��OBN+S��OAM��
= ![]() MNPH��
MNPH�� ![]() ONyB+
ONyB+ ![]() OM|yA|��
OM|yA|��
= ![]() ��2k��k��
��2k��k�� ![]() ��k+1����1+
��k+1����1+ ![]() ��k��1����1��
��k��1����1��
=k2��1��
��0��k��1ʱ����ͼ2��

S��PAB=S��OBN��S��PMN+S��OAM��
= ![]() ONyB��k2+
ONyB��k2+ ![]() OM|yA|��
OM|yA|��
= ![]() ��k+1����1��k2+
��k+1����1��k2+ ![]() ��1��k����1��
��1��k����1��
=1��k2
���������⣺��1������������������ͼ��ĶԳ��Կ�֪����A��B����ԭ��O�Գƣ�
��A�����������k����1����
��B���������k��1����
���Դ��ǣ���k��1����
2����֤���������£���P��m�� ![]() ����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
�� 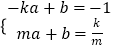 ��
��
��ã� 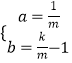 ��
��
��ֱ��PA�Ľ���ʽΪy= ![]() x+
x+ ![]() ��1��
��1��
��y=0ʱ��x=m��k��
��M���������m��k��0����
����P��PH��x����H����ͼ1��ʾ��
��P��������m�� ![]() ����
����
��H���������m��0����
��MH=xH��xM=m����m��k��=k��
ͬ���ɵã�HN=k��
��MH=HN��
��PM=PN��
���Դ��ǣ� 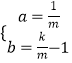 ��y=
��y= ![]() x+
x+ ![]() ��1��
��1��
�����㾫����������Ĺؼ��������ⷴ����������ͼ������֪ʶ�����շ�����������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�㣬�Լ��Է��������������ʵ����⣬�˽�����:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ�����������