题目内容
【题目】已知:如图,反比例函数 ![]() 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).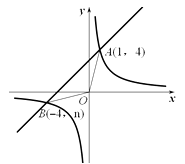
(1)求△OAB的面积;
(2)根据图象,直接写出不等式 ![]() 的解集.
的解集.
【答案】
(1)解:把A点(1,4)分别代入反比例函数 ![]() ,一次函数y=x+b,
,一次函数y=x+b,
得k=1×4,1+b=4,
解得k=4,b=3,
∴一次函数解析式是y=x+3;
如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴ ![]()
(2)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时, ![]()
【解析】(1)求出直线AB的解析式 ,求出与y轴的交点,通过分割,把△OAB的面积分成两部分,即S Δ A O B = S Δ A O C + S Δ B O C,进而求出面积;(2)利用数形结合的思想,不等式的解集转化为两图像的交点问题,即A点的左侧部分与B的右侧部分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目