题目内容
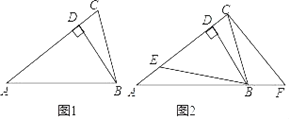
【题目】如图1,在![]() 和
和![]() 中,
中, ![]() ,
,![]() ,
,![]() .
.

(1)若![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
(2)在第(1)问的条件下,求证: ![]() ;
;
(3)将![]() 绕点
绕点![]() 顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
顺时针旋转得到图2,那么第(2)问中的结论是否依然成立?若成立,请证明你的结论:若不成立,请说明理由.
【答案】(1)见解析;(2)见解析;(3)成立,理由见解析
【解析】
(1)根据SAS得出△BAD≌△CAE;
(2)根据△BAD≌△CAE,得出∠ABD=∠ACE,根据直角三角形两锐角互余和对顶角相等即可得出答案;
(3)延长BD交CE于点M,交AC于点F.根据SAS证明ΔBAD≌ΔCAE,得出∠ABD=∠ACE,根据直角三角形两锐角互余和对顶角相等即可得出答案.
(1)∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴ΔBAD≌ΔCAE.
(2)∵ΔBAD≌ΔCAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,
∴∠ABD+∠AFB=90°.
∵∠AFB=∠CFD,
∴∠ACE+∠CFD=90°,
∴∠CDF=90°,
∴BD⊥CE.
(3)成立.理由如下:
延长BD交CE于点M,交AC于点F.
∵∠BAC=∠DAE=90°,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴ΔBAD≌ΔCAE,
∴∠ABD=∠ACE.
∵∠BAC=90°,
∴∠ABD+∠AFB=90°.
∵∠AFB=∠CFM,
∴∠CMF=90°,
∴BD⊥CE.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目