题目内容
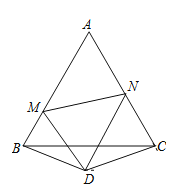
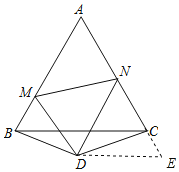
【题目】如图,在△ABC和△DBC中,∠A=40°,AB=AC=2,∠BDC=140°,BD=CD,以点D为顶点作∠MDN=70°,两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为___________.
【答案】4
【解析】
延长AC至E,使CE=BM,连接DE.证明△BDM≌△CDE(SAS),得出MD=ED,∠MDB=∠EDC,证明△MDN≌△EDN(SAS),得出MN=EN=CN+CE,进而得出答案.
延长AC至E,使CE=BM,连接DE.
∵BD=CD,且∠BDC=140°,
∴∠DBC=∠DCB=20°,
∵∠A=40°,AB=AC=2,
∴∠ABC=∠ACB=70°,
∴∠MBD=∠ABC+∠DBC=90°,
同理可得∠NCD=90°,
∴∠ECD=∠NCD=∠MBD=90°,
在△BDM和△CDE中,
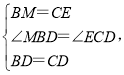
∴△BDM≌△CDE(SAS),
∴MD=ED,∠MDB=∠EDC,
∴∠MDE=∠BDC=140°,
∵∠MDN=70°,
∴∠EDN=70°=∠MDN,
在△MDN和△EDN中,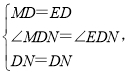
∴△MDN≌△EDN(SAS),
∴MN=EN=CN+CE,
∴△AMN的周长=AM+MN+AN=AM+CN+CE+AN=AM+AN+CN+BM=AB+AC=4;
故答案为:4.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目