��Ŀ����
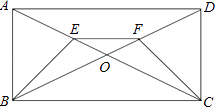
����Ŀ�����һ������εĸ��߶���ȣ��Ҹ��ڽ�Ҳ����ȣ���ô�������ξͽ���������Σ���ͼ������һ��������Σ��۲�ÿ����������С����ı仯���������������⣮

��1��������ı���������
������εı��� | 3 | 4 | 5 | 6 | ���� | 18 |
�����Ķ��� | �� �� | �� �� | �� �� | �� �� | ���� | �� �� |
��2�����ݹ��ɣ��Ƿ����һ����n���Σ�ʹ���еġ���=20���������ڣ�ֱ��д��n��ֵ���������ڣ���˵�����ɣ�
��3�����ݹ��ɣ��Ƿ����һ����n���Σ�ʹ���еġ���=21���������ڣ�ֱ��д��n��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��60�㣬45�㣬36�㣬30�㣬10�㣻��2��������������ű��Σ���ʹ���еġ���=20�㣻��3�������ڣ����ɼ�����
��������
��1�����ݶ�����ڽǺ�ʽ�������ε��ڽǺͣ��ٸ����������ڽǺͶ���������ɣ�
��2�����ݱ��еĽ���ó����ɣ����ݹ��ɵó����̣�������̵Ľ⼴����
��3�����ݱ��еĽ���ó����ɣ����ݹ��ɵó����̣�������̵Ľ⼴����
��1��������£�
������εı��� | 3 | 4 | 5 | 6 | ���� | 18 |
�����Ķ��� | 60�� | 45�� | 36�� | 30�� | ���� | 10�� |
�ʴ�Ϊ��60�㣬45�㣬36�㣬30�㣬10�㣻
��2������һ����n���Σ�ʹ���еġ���=20����
�����ǣ���������ã�![]() =20�㣬
=20�㣬
��ã�n=9��
��������������ű��Σ���ʹ���еġ���=20�㣻
��3�������ڣ��������£�
��������� n ����ʹ�á���=21������ ![]() ��
��
��ã�![]() ���� n ����������
���� n ����������
���Բ������� n ����ʹ�á���=21�㣮

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�