题目内容
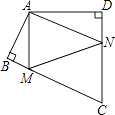
【题目】(方程思想)如图，在铁路CD同侧有两个村庄A，B，它们到铁路的距离分别是15 km和10 km，作AC⊥CD，BD⊥CD，垂足分别为C，D，且CD＝25 km.已知铁路旁有一个农副产品收购站E，且AE＝BE，求CE的长．
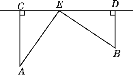
【答案】CE＝10 km.
【解析】
在Rt△DBE和Rt△CAE中，根据勾股定理得：AC2＋CE2＝AE2和BD2＋DE2＝BE2，再由AE＝BE得出AE2＝BE2，从而得出AC2＋CE2＝BD2＋DE2，设出CE的长，可将AE和BE的长表示出来，列出等式进行求解即可．
解：在Rt△ACE中，根据勾股定理得AC2＋CE2＝AE2.
在Rt△BDE中，根据勾股定理得BD2＋DE2＝BE2.
∵AE＝BE，
∴AE2＝BE2，
即AC2＋CE2＝BD2＋DE2.
设CE＝x km，
则152＋x2＝102＋(25－x)2，
解得x＝10.
∴CE＝10 km.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．
（1）将下面的表格补充完整：
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
（2）根据规律，是否存在一个正n边形，使其中的∠α=20°？若存在，直接写出n的值；若不存在，请说明理由．
（3）根据规律，是否存在一个正n边形，使其中的∠α=21°？若存在，直接写出n的值；若不存在，请说明理由．
