题目内容
【题目】计算题。 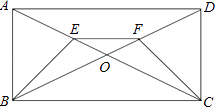
(1)用适当的方法解下列一元二次方程:x2﹣6x+1=0.
(2)如图,已知E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF,求证:BE=CF.
【答案】
(1)解:x2﹣6x+1=0.
移项得,x2﹣6x=﹣1,
配方得,x2﹣6x+9=﹣1+9,
∴(x﹣3)2=8,
∴x﹣3=±2 ![]() ,
,
∴x1=3+2 ![]() ,x2=3﹣2
,x2=3﹣2 ![]()
(2)证明:∵矩形ABCD的对角线为AC和BD,
∴AO=CO=BO=DO,
∵E、F分别是矩形ABCD的对角线AC和BD上的点,AE=DF,
∴EO=FO,
在△BOE和△COF中, 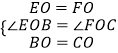 ,
,
∴△BOE≌△COF(SAS),
∴BE=CF.
【解析】(1)用配方法解一元二次方程,首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式.(2)根据矩形对角线的性质,矩形对角线互相平分且相等,可知EO=FO,BO=CO,∠BOE=∠COF,可知△BOE≌△COF,即可得出BE=CF.
【考点精析】利用矩形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.