题目内容
【题目】如图,点D为码头,A,B两个灯塔与码头的距离相等,DA,DB为海岸线,一轮船离开码头,计划沿∠ADB的平分线航行,在航行途中C点处,测得轮船与灯塔A和灯塔B的距离相等.试问:轮船航行是否偏离指定航线?请说明理由.
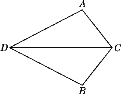
【答案】轮船航行没有偏离指定航线.理由见解析.
【解析】
试题只要证明轮船与D点的连线平分∠ADB就说明轮船没有偏离航线,也就是证明∠ADC=∠BDC,证角相等,常常通过把角放到两个三角形中,利用题目条件证明这两个三角形全等,从而得出对应角相等.
试题解析:
答:轮船航行没有偏离指定航线。
理由是:在⊿ADC与⊿BDC中,
∵AD=BD,DC=DC,AC=BC
∴⊿ADC≌⊿BDC(SSS)
∴∠ADC=∠BDC
∴轮船航线DC即为∠ADB的角平分线
故轮船航行没有偏离指定航线。
考点:1.全等三角形的性质;2. 全等三角形的应用.

练习册系列答案
相关题目
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.