题目内容
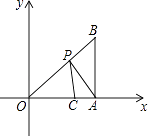
【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.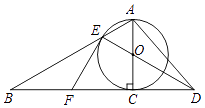
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离.
【答案】
(1)
证明:连接CE,如图所示:
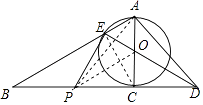
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°.
∵点F为BC的中点,
∴EF=BF=CF.
∴∠FEC=∠FCE.
∵OE=OC,
∴∠OEC=∠OCE.
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°.
∴EF是⊙O的切线;
(2)
解:设P点到直线AD的距离为d,记△PAD的面积S△PAD,
则有:S△PAD= ![]() ADd=
ADd= ![]() PDAC,
PDAC,
∴d= ![]() ①
①
∵⊙O的半径为3,∠B=30°,
∴∠BAC=60°,AC=6,AB=12,
由勾股定理得BC=6 ![]() ,
,
∴PC=3 ![]() ,
,
∵O,P分别是AC,BC的中点,
∴OP∥AB,
∴∠OPC=∠B=30°,
∵OE=OA,∠OAE=60°,
∴△OEA为等边三角形,
∴∠EOA=60°,
∴∠ODC=90°﹣∠COD=90°﹣∠EOA=30°,
∴∠ODC=∠OPC=30°,
∴OP=OD,
∵OC⊥PD,
∴CD=PC=3 ![]() ,
,
在Rt△ACD中,由勾股定理得:AD= ![]() =3
=3 ![]() ,
,
将以上数据代入①得:d= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.(2)设P点到直线AD的距离为d,记△PAD的面积S△PAD , 根据三角形的面积得到d= ![]() ①由勾股定理得BC=6
①由勾股定理得BC=6 ![]() ,根据平行线的性质得到∠OPC=∠B=30°,推出△OEA为等边三角形,得到∠EOA=60°,在Rt△ACD中,由勾股定理得:AD=
,根据平行线的性质得到∠OPC=∠B=30°,推出△OEA为等边三角形,得到∠EOA=60°,在Rt△ACD中,由勾股定理得:AD= ![]() =3
=3 ![]() ,将以上数据代入①得即可得到结论.
,将以上数据代入①得即可得到结论.

【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.

(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | 18 |
∠α的度数 |
|
|
|
| …… |
|
(2)根据规律,是否存在一个正n边形,使其中的∠α=20°?若存在,直接写出n的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.