题目内容
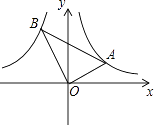
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点A的坐标为(﹣1,0),与y轴交于点C(0,3),作直线BC.动点P在x轴上运动,过点P作PM⊥x轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.
(Ⅰ)求抛物线的解析式和直线BC的解析式;
(Ⅱ)当点P在线段OB上运动时,求线段MN的最大值;
(Ⅲ)当以C、O、M、N为顶点的四边形是平行四边形时,直接写出m的值.
【答案】解:(Ⅰ)∵抛物线过A、C两点,
∴代入抛物线解析式可得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3,
令y=0可得,﹣x2+2x+3=0,解x1=﹣1,x2=3,
∵B点在A点右侧,
∴B点坐标为(3,0),
设直线BC解析式为y=kx+s,
把B、C坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线BC解析式为y=﹣x+3;
(Ⅱ)∵PM⊥x轴,点P的横坐标为m,
∴M(m,﹣m2+2m+3),N(m,﹣m+3),
∵P在线段OB上运动,
∴M点在N点上方,
∴MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,MN有最大值,MN的最大值为
时,MN有最大值,MN的最大值为 ![]() ;
;
(Ⅲ)∵PM⊥x轴,
∴MN∥OC,
当以C、O、M、N为顶点的四边形是平行四边形时,则有OC=MN,
当点P在线段OB上时,则有MN=﹣m2+3m,
∴﹣m2+3m=3,此方程无实数根,
当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,
∴m2﹣3m=3,解得m= ![]() 或m=
或m= ![]() ,
,
综上可知当以C、O、M、N为顶点的四边形是平行四边形时,m的值为 ![]() 或
或 ![]() .
.
【解析】(1)把A、C两点的坐标代入抛物线的解析式中列方程组可求得b,c的值,令y=0,解方程可得B点的坐标,利用待定系数法求直线BC的解析式;(2)根据解析式表示出M、N两点的坐标,其纵坐标的差就是MN的长,配方后求得最值即可;(3)分两种情况:当点P在线段OB上时,则有MN=﹣m2+3m,当点P不在线段OB上时,则有MN=﹣m+3﹣(﹣m2+2m+3)=m2﹣3m,根据MN=3列方程解出即可。
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案