题目内容
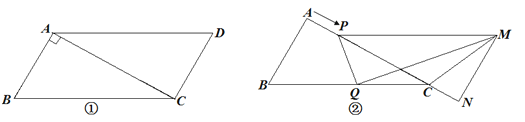
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.
(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明；
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论，请用简洁的语言表达BD与DE,CE的数量关系。
【答案】(1)、证明过程见解析；(2)、BD=DE–CE；证明过程见解析；(3)、BD=DE–CE；(4)、当B,C在AE的同侧时，BD=DE–CE；当B,C在AE的异侧时，BD=DE+CE.
【解析】
试题分析：(1)、根据垂直得出∠ADB=∠CEA=90°，结合∠BAC=90°得出∠ABD=∠CAE，从而证明出△ABD和△ACE全等，根据全等得出BD=AE,AD=EC，然后得出答案；(2)、根据第一题同样的方法得出△ABD和△ACE全等，根据全等得出BD=AE,AD=EC，然后得出结论；(3)、根据同样的方法得出结论；(4)、根据前面的结论得出答案.
试题解析：(1)∵BD⊥AE，CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90° 又∵∠BAC=90°
∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE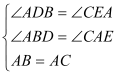
∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE+CE
(2)、∵BD⊥AE，CE⊥AE ∴∠ADB=∠CEA=90° ∴∠ABD+∠BAD=90°
又∵∠BAC=90°∴∠EAC+∠BAD=90° ∴∠ABD=∠CAE
在△ABD与△ACE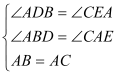 ∴△ABD≌△ACE ∴BD=AE,AD=EC ∴BD=DE–CE
(3)、BD=DE–CE
(4)、归纳：由（1）（2）（3）可知：当B,C在AE的同侧时，BD = DE –CE；当B,C在AE的异侧时，∴BD=DE+CE
