题目内容
【题目】如图,点A是反比例函数y= ![]() (x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y=
(x>0)上的一个动点,连接OA,过点O作OB⊥OA,并且使OB=2OA,连接AB,当点A在反比函数图象上移动时,点B也在某一反比例函数图象y= ![]() 上移动,k的值为( )
上移动,k的值为( )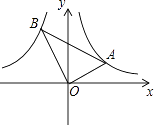
A.2
B.﹣2
C.4
D.﹣4
【答案】D
【解析】解:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
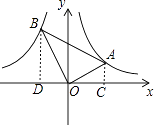
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=( ![]() )2,
)2,
∵OB=2OA,
∴S△AOC:S△BOD= ![]() ,
,
∵S△AOC= ![]() OCAC=
OCAC= ![]() ×1=
×1= ![]() ,S△BOD=
,S△BOD= ![]() ODBD=
ODBD= ![]() |k|,
|k|,
∴k=﹣4,
所以答案是:D.
【考点精析】根据题目的已知条件,利用比例系数k的几何意义和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?






