题目内容
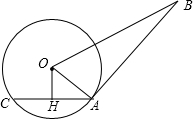
如图，AB是⊙O的切线，A为切点，AC是⊙O的弦，过O作OH⊥AC于点H．若OH=2，AB=12，BO=13．则sin∠OAC的值为______．
∵AB是⊙O的切线，
∴∠OAB=90°，又AB=12，BO=13，
根据勾股定理得：OA=
=5，又OH=2，
在直角三角形OAH中，根据锐角三角函数的定义得：
sin∠OAC=
=
．
故答案为：
∴∠OAB=90°，又AB=12，BO=13，
根据勾股定理得：OA=
| 132-122 |
在直角三角形OAH中，根据锐角三角函数的定义得：
sin∠OAC=
| OH |
| OA |
| 2 |
| 5 |
故答案为：
| 2 |
| 5 |
练习册系列答案
相关题目
延长线分别交AC、BC于点G、F．
O与⊙O交于点D，与PA的延长线交于点E．
OE=1cm，DF=4cm．
于点B．点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线AP，作EH⊥AP于H．