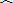题目内容
如图，D是半径为R的⊙O上一点，过点D作⊙O的切线交直径AB的延长线于点C，下列四个条件：①AD=CD；②∠A=30°；③∠ADC=120°；④DC=
R．其中，使得BC=R的有（ ）
| 3 |
| A．①② | B．①③④ | C．②③④ | D．①②③④ |
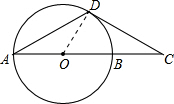
连接OD，则OD⊥CD；
①∵AD=DC，
∴∠A=∠C，
∴∠DOC=2∠A=2∠C；
在Rt△ODC中，∠C+∠DOC=90°，
即∠A=∠C=30°，
∴OC=2OD，OB+BC=2OD，由于OB=OD，故BC=OB=R，①正确；
②由①可知：当∠A=30°时，可以得到BC=R，故②正确；
③∠ADC=120°，则∠A=∠C=
（180°-∠ADC）=30°，
由①②知，当∠A=30°时，BC=R成立，故③正确；
④DC=
R，则tan∠C=
=
，即∠A=∠C=30°，
故④正确；
所以四个结论都能是BC=R成立，
故选D．
①∵AD=DC，
∴∠A=∠C，
∴∠DOC=2∠A=2∠C；
在Rt△ODC中，∠C+∠DOC=90°，
即∠A=∠C=30°，
∴OC=2OD，OB+BC=2OD，由于OB=OD，故BC=OB=R，①正确；
②由①可知：当∠A=30°时，可以得到BC=R，故②正确；
③∠ADC=120°，则∠A=∠C=
| 1 |
| 2 |
由①②知，当∠A=30°时，BC=R成立，故③正确；
④DC=
| 3 |
| OD |
| CD |
| ||
| 3 |
故④正确；
所以四个结论都能是BC=R成立，
故选D．
练习册系列答案
初中学业考试导与练系列答案
相关题目
C，垂足为点F．
