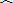题目内容
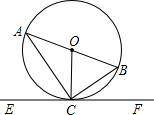
在坐标平面内,半径为R的⊙O与x轴交于点D(1,0)、E(5,0),与y轴的正半轴相切 于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.
于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.
(1)求圆心C的坐标及半径R的值;
(2)△POA和△PHE随点P的运动而变化,若它们全等,求a的值;若给定a=6,试判定直线AP与⊙C的位置关系(要求说明理由).
 于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.
于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.(1)求圆心C的坐标及半径R的值;
(2)△POA和△PHE随点P的运动而变化,若它们全等,求a的值;若给定a=6,试判定直线AP与⊙C的位置关系(要求说明理由).
(1)连接BC,则BC⊥y轴.
取DE中点M,连CM,则CM⊥x轴.
∵OD=1,OE=5,
∴OM=3.
∵OB2=OD•OE=5,
∴OB=
.
∴圆心C(3,
),半径R=3.
(2)∵△POA≌△PHE,
∴PA=PE.
∵OA=OB=
,OE=5,OP=a,
∴PA2=a2+5,
PE2=(5-a)2,
∴a2+5=(a-5)2,
a=2.
(3)解法一:
过点A作⊙C的切线AT(T为切点),交x轴正半轴于Q.
设Q(m,0),则QE=m-5,QD=m-1,
QT=QA-AT=QA-AB=
-2
.
由QT2=QE•QD,
得(
-2
)2=(m-5)(m-1),
2
=3m+10,
11m2-60m=0.
∵m>0,
∴m=
.
∵a=6,点P(6,0),在点Q(
,0)的右侧,
∴直线AP与⊙C相离.
解法二:
设射线AP、BC交于点F,作CT⊥AF于T.
∵△AOP∽△CTF,
∴
=
.
而AO=
,AP=
,
CF=BF-BC=12-3=9,
∴
=
,
CT=
>
=3=R,
∴直线AP与⊙C相离.

取DE中点M,连CM,则CM⊥x轴.
∵OD=1,OE=5,
∴OM=3.
∵OB2=OD•OE=5,
∴OB=
| 5 |
∴圆心C(3,
| 5 |
(2)∵△POA≌△PHE,
∴PA=PE.
∵OA=OB=
| 5 |
∴PA2=a2+5,
PE2=(5-a)2,
∴a2+5=(a-5)2,
a=2.
(3)解法一:

过点A作⊙C的切线AT(T为切点),交x轴正半轴于Q.
设Q(m,0),则QE=m-5,QD=m-1,
QT=QA-AT=QA-AB=
| m2+5 |
| 5 |
由QT2=QE•QD,
得(
| m2+5 |
| 5 |
2
| 5(m2+5) |
11m2-60m=0.
∵m>0,
∴m=
| 60 |
| 11 |
∵a=6,点P(6,0),在点Q(
| 60 |
| 11 |
∴直线AP与⊙C相离.
解法二:
设射线AP、BC交于点F,作CT⊥AF于T.

∵△AOP∽△CTF,
∴
| CT |
| CF |
| AO |
| AP |
而AO=
| 5 |
| 41 |
CF=BF-BC=12-3=9,
∴
| CT |
| 9 |
| ||
|
CT=
9
| ||
|
9
| ||
|
∴直线AP与⊙C相离.


练习册系列答案
相关题目
 C,垂足为点F.
C,垂足为点F.