题目内容
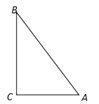
【题目】新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在RtΔABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为 ________.
【答案】4或![]()
【解析】
试题由到两个点距离相等的点在这两个点为端点的线段的垂直平分线上,则点P可在三角形任一边的垂直平分线上,则点P可是三角形任一边的垂直平分线与BC的交点,根据题意分三种情况进行讨论:①P在BC的垂直平分线上;②P在AB的垂直平分线上;③P在AC的垂直平分线上.
解:在RtΔABC中,∠C=90°,AB=10,AC=6,则BC=![]() =8.
=8.
由到两个点距离相等的点在这两个点为端点的线段的垂直平分线上,则点P可在三角形任一边的垂直平分线上,根据题意分三种情况进行讨论:
①P在BC的垂直平分线上,则P为BC中点,则PC=![]() BC=4;
BC=4;
②P在AB的垂直平分线上,设PC=x,则PB=PA=8-x,
在Rt△PAC中,AC2+PC2=PA2,即36+x2=(8-x)2,解得x=![]() ,即PC=
,即PC=![]() ;
;
③P在AC的垂直平分线上,又AC的垂直平分线平行于BC,则P不可能在BC上,此时不成立.
故答案为4或![]() .
.

练习册系列答案
相关题目