题目内容
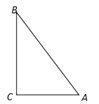
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
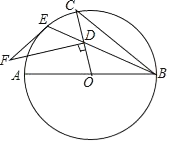
【答案】(1)详见解析;(2)![]()
【解析】
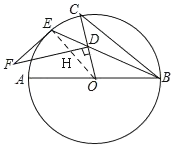
(1)连接OE交DF于点H,由切线的性质得出∠F+∠EHF =90,由FD⊥OC得出∠DOH+∠DHO =90,依据对顶角的定义得出∠EHF=∠DHO,从而求得∠F=∠DOH,依据∠CBE=![]() ∠DOH,从而即可得证;
∠DOH,从而即可得证;
(2)依据圆周角定理及其推论得出∠F=∠COE=2∠CBE =30°,求出OD的值,利用锐角三角函数的定义求出OH的值,进一步求得HE的值,利用锐角三角函数的定义进一步求得EF的值.
(1)证明:连接OE交DF于点H,
∵EF是⊙O的切线,OE是⊙O的半径,
∴OE⊥EF.
∴∠F+∠EHF=90°.
∵FD⊥OC,
∴∠DOH+∠DHO=90°.
∵∠EHF=∠DHO,
∴∠F=∠DOH.
∵∠CBE=![]() ∠DOH,
∠DOH,
∴![]()
(2)解:∵∠CBE=15°,
∴∠F=∠COE=2∠CBE=30°.
∵⊙O的半径是![]() ,点D是OC中点,
,点D是OC中点,
∴![]() .
.
在Rt△ODH中,cos∠DOH=![]() ,
,
∴OH=2.
∴![]() .
.
在Rt△FEH中,![]()
∴![]()

 愉快的寒假南京出版社系列答案
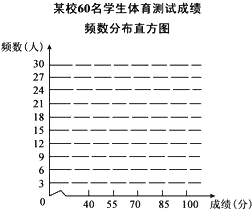
愉快的寒假南京出版社系列答案【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.