题目内容
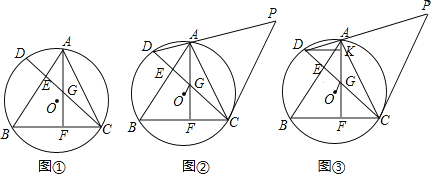
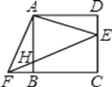
【题目】如图，△ADE绕正方形ABCD的顶点A顺时针旋转90°，得△ABF，连接EF交AB于H，有如下五个结论①AE⊥AF；②EF：AF=
：1；③AF2=FHFE；④∠AFE=∠DAE+∠CFE ⑤ FB：FC=HB：EC．则正确的结论有（ ）
A.2个B.3个C.4个D.5个
【答案】C
【解析】
由旋转性质得到△AFB≌△AED，再根据相似三角对应边的比等于相似比，即可分别求得各选项正确与否.
解：由题意知，△AFB≌△AED
∴AF=AE，∠FAB=∠EAD，∠FAB+∠BAE=∠EAD+∠BAE=∠BAD=90°.
∴AE⊥AF，故此选项①正确；
∴∠AFE=∠AEF=∠DAE+∠CFE，故④正确；
∵△AEF是等腰直角三角形，有EF:AF=
：1，故此选项②正确；
∵△AEF与△AHF不相似，
∴AF2=FH·FE不正确.故此选项③错误，
∵HB//EC，
∴△FBH∽△FCE，
∴FB:FC=HB:EC，故此选项⑤正确.
故选：C
练习册系列答案
智能训练练测考系列答案
相关题目
