ЬтФПФкШн
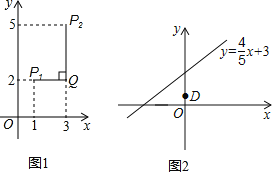
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЖдгкШЮвтСНЕуPЃЈx1ЃЌy1ЃЉгыP2ЃЈx2ЃЌy2ЃЉЕФЁАзюМбОрРыЁБЃЌИјГіШчЯТЖЈвхЃК
Шє|x1Љx2|Ён|y1Љy2|ЃЌдђЕуP1гыЕуP2ЕФЁАзюМбОрРыЁБЮЊ|x1Љx2|ЃЛ
Шє|x1Љx2|ЃМ|y1Љy2|ЃЌдђЕуP1гыЕуP2ЕФЁАзюМбОрРыЁБЮЊ|y1Љy2|ЃЛ
Р§ШчЃКЕуP1ЃЈ1ЃЌ2ЃЉЃЌЕуP2ЃЈ3ЃЌ5ЃЉЃЌвђЮЊ|1Љ3|ЃМ|2Љ5|ЃЌЫљвдЕуP1гыЕуP2ЕФЁАзюМбОрРыЁБЮЊ|2Љ5|ЃН3ЃЌвВОЭЪЧЭМ1жаЯпЖЮP1QгыЯпЖЮP2QГЄЖШЕФНЯДѓжЕЃЈЙ§ЕуP1ЦНаагкxжсЕФжБЯпгыЙ§ЕуP2ДЙжБгкxжсЕФжБЯпНЛгкЕуQЃЉЃЎ
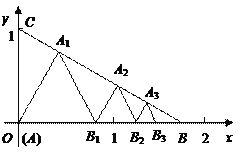
ЃЈ1ЃЉвбжЊЕуAЃЈЉ![]() ЃЌ0ЃЉЃЌBЮЊyжсЩЯЕФвЛИіЖЏЕуЃЎ
ЃЌ0ЃЉЃЌBЮЊyжсЩЯЕФвЛИіЖЏЕуЃЎ
ЂйШєЕуAгыЕуBЕФЁАзюМбОрРыЁБЮЊ3ЃЌаДГіТњзуЬѕМўЕФЕуBЕФзјБъЃЛ
ЂкжБНгаДГіЕуAгыЕуBЕФЁАзюМбОрРыЁБЕФзюаЁжЕЃЛ
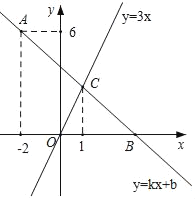
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊЕуCЪЧжБЯпyЃН![]() x+3ЩЯЕФвЛИіЖЏЕуЃЌЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌЧѓЕуCгыЕуDЕФЁАзюМбОрРыЁБЕФзюаЁжЕМАЯргІЕФЕуCЕФзјБъЃЎ
x+3ЩЯЕФвЛИіЖЏЕуЃЌЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌЧѓЕуCгыЕуDЕФЁАзюМбОрРыЁБЕФзюаЁжЕМАЯргІЕФЕуCЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ0ЃЌ3ЃЉЃЌЃЈ0ЃЌЉ3ЃЉЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
(1) ЂйЕуAгыЕуBЕФКсзјБъВюЕФОјЖджЕЮЊ![]() ЃЌЁАзюМбОрРыЁБЮЊ3ЃЌвђДЫПЩвдAЁЂBзнзјБъЕФВюЕФОјЖджЕЮЊ3ЃЌДгЖјЧѓГіBЕузјБъЕФСНжжЧщПіЃЛ
ЃЌЁАзюМбОрРыЁБЮЊ3ЃЌвђДЫПЩвдAЁЂBзнзјБъЕФВюЕФОјЖджЕЮЊ3ЃЌДгЖјЧѓГіBЕузјБъЕФСНжжЧщПіЃЛ
ЂкИљОнЬтвтЕУЃК|Љ![]() Љ0|Ён|0Љy|ЃЌЧѓГіЁАзюМбОрРыЁБЕФзюаЁжЕЮЊ
Љ0|Ён|0Љy|ЃЌЧѓГіЁАзюМбОрРыЁБЕФзюаЁжЕЮЊ![]()
ЃЈ2ЃЉЩшЕуCЃЈmЃЌ![]() m+3ЃЉЃЌЧвЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌЕБ|mЉ0|ЃН|
m+3ЃЉЃЌЧвЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌЕБ|mЉ0|ЃН|![]() m+3Љ1|ЃН|
m+3Љ1|ЃН|![]() m+2|ЪБЃЌЕуCгыЕуDЕФЁАзюМбОрРыЁБгазюаЁжЕЃЌДгЖјЧѓГіCЕузјБъ.
m+2|ЪБЃЌЕуCгыЕуDЕФЁАзюМбОрРыЁБгазюаЁжЕЃЌДгЖјЧѓГіCЕузјБъ.
НтЃКЃЈ1ЃЉЂйЁпЕуBЮЊyжсЩЯЕФвЛИіЖЏЕу
ЁрЩшЕуBЕФзјБъЮЊЃЈ0ЃЌyЃЉ
Ёп|Љ![]() Љ0|ЃН
Љ0|ЃН![]() Ёй3
Ёй3
Ёр|0Љy|ЃН3
ЁрyЃНЁР3
ЁрЕуBЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌЃЈ0ЃЌЉ3ЃЉ
ЂкЩшЕуBЕФзјБъЮЊЃЈ0ЃЌyЃЉЃЌ
ИљОнЬтвтЕУЃК|Љ![]() Љ0|Ён|0Љy|
Љ0|Ён|0Љy|
Ёр|yЉ0|Ём![]()
ЁрЕуAгыЕуBЕФЁАзюМбОрРыЁБЕФзюаЁжЕЮЊ![]()
ЃЈ2ЃЉЁпЕуCЪЧжБЯпyЃН![]() x+3ЩЯЕФвЛИіЖЏЕуЃЌ
x+3ЩЯЕФвЛИіЖЏЕуЃЌ
ЁрЩшЕуCЃЈmЃЌ![]() m+3ЃЉЃЌЧвЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌ
m+3ЃЉЃЌЧвЕуDЕФзјБъЪЧЃЈ0ЃЌ1ЃЉЃЌ
ЁрЕБ|mЉ0|ЃН|![]() m+3Љ1|ЃН|
m+3Љ1|ЃН|![]() m+2|ЪБЃЌЕуCгыЕуDЕФЁАзюМбОрРыЁБгазюаЁжЕЃЌ
m+2|ЪБЃЌЕуCгыЕуDЕФЁАзюМбОрРыЁБгазюаЁжЕЃЌ
ЕБmЁмЉ![]() ЪБЃЌЉmЃНЉ
ЪБЃЌЉmЃНЉ![]() mЉ2
mЉ2
НтЕУЃКmЃН10ЃЈВЛКЯЬтвтЩсШЅЃЉ
ЕБЉ![]() ЃМmЃМ0ЪБЃЌЉmЃН
ЃМmЃМ0ЪБЃЌЉmЃН![]() m+2
m+2
НтЕУЃКmЃНЉ![]()
ЕБmЃО0ЪБЃЌmЃН![]() m+2
m+2
НтЕУЃКmЃН10
Ёр|m|ЃН10Лђ![]()
ЁрЕуCгыЕуDЕФЁАзюМбОрРыЁБЕФзюаЁжЕЮЊ![]() ЃЌ
ЃЌ
ЁрЕуCзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ

 ШЋФмСЗПМОэЯЕСаД№АИ
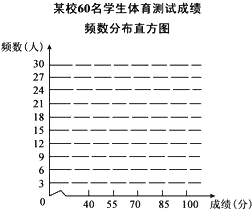
ШЋФмСЗПМОэЯЕСаД№АИЁОЬтФПЁПФГаЃЮЊСЫИќКУЕФПЊеЙЁАбЇаЃЬиЩЋЬхг§НЬг§ЁБЃЌДгШЋаЃАЫФъМЖЕФИїАрЗжБ№ЫцЛњГщШЁСЫ5УћФаЩњКЭ5УћХЎЩњЃЌзщГЩСЫвЛИіШнСПЮЊ60ЕФбљБОЃЌНјааИїЯюЬхг§ЯюФПЕФВтЪдЃЌСЫНтЫћУЧЕФЩэЬхЫижЪЧщПіЃЎЯТБэЪЧећРэбљБОЪ§ОнЃЌЕУЕНЕФЙигкУПИіИіЬхЕФВтЪдГЩМЈЕФВПЗжЭГМЦБэЁЂЭМЃКФГаЃ60УћбЇЩњЬхг§ВтЪдГЩМЈЦЕЪ§ЗжВМБэ
ГЩМЈ | ЛЎМЧ | ЦЕЪ§ | АйЗжБШ |
гХау | е§е§е§ | a | 30% |
СМКУ | е§е§е§е§е§е§ | 30 | b |
КЯИё | е§ | 9 | 15% |
ВЛКЯИё |
| 3 | 5% |
КЯМЦ | 60 | 60 | 100% |
ЃЈЫЕУїЃК40ЉЉЉ55ЗжЮЊВЛКЯИёЃЌ55ЉЉЉ70ЗжЮЊКЯИёЃЌ70ЉЉЉ85ЗжЮЊСМКУЃЌ85ЉЉЉ100ЗжЮЊгХауЃЉЧыИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжаЕФa=_____ЃЌb=_____ЃЛ
ЃЈ2ЃЉЧыИљОнЦЕЪ§ЗжВМБэЃЌЛГіЯргІЕФЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШчЙћИУаЃАЫФъМЖЙВга150УћбЇЩњЃЌИљОнвдЩЯЪ§ОнЃЌЙРМЦИУаЃАЫФъМЖбЇЩњЩэЬхЫижЪСМКУМАвдЩЯЕФШЫЪ§ЮЊ_____ЃЎ